题目内容
已知直线y=x-3与函数
的图象相交于点（a，b），则a2+b2的值是
- A.13
- B.11
- C.7
- D.5
A
分析：把交点坐标代入两个函数解析式，得到a和b的相关式子，再整理即可．
解答：∵直线y=x-3与函数的图象相交于点（a，b），
∴b=a-3，ab=2，
∴a2+b2=（b-a）2+2ab=13．
故选A．
点评：点在函数图象上，点的横纵坐标应适合函数解析式，解决本题的关键是得到和a，b相关的式子．
分析：把交点坐标代入两个函数解析式，得到a和b的相关式子，再整理即可．
解答：∵直线y=x-3与函数
的图象相交于点（a，b），∴b=a-3，ab=2，
∴a2+b2=（b-a）2+2ab=13．
故选A．
点评：点在函数图象上，点的横纵坐标应适合函数解析式，解决本题的关键是得到和a，b相关的式子．
练习册系列答案
阅读快车系列答案
相关题目
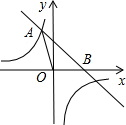如图，已知直线y=-x+4与反比例函数
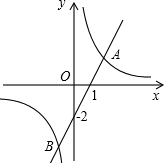已知直线y=2x-2与双曲线图
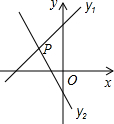如图，已知直线y1=x+m与y2=kx-1相交于点P（-1，1），则关于x的不等式x+m＞kx-1的解集的是