题目内容
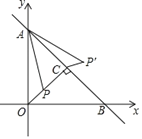
【题目】如图,已知点![]() ,
,![]() ,
,![]() ,动点
,动点![]() 在线段
在线段![]() 上,点
上,点![]() 、
、![]() 、
、![]() 按逆时针顺序排列,且
按逆时针顺序排列,且![]() ,
,![]() ,当点
,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则点
时,则点![]() 运动的路径长为_______.
运动的路径长为_______.

【答案】6
【解析】
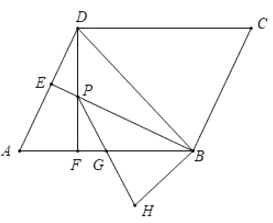
当点P与点A重合时,作MF⊥x轴,CH⊥x轴交AB于E,作BG⊥CH于G,连接ME,取MC的中点D以CD为半径作圆,连接DE、DA,先求出点E坐标为(-1,2),证明△AMF≌△CAH,得到点M(-7,2),当点P与点B重合时,点M与点E重合,即可得到答案.
如图,当点P与点A重合时,作MF⊥x轴,CH⊥x轴交AB于E,作BG⊥CH于G,连接ME,取MC的中点D以CD为半径作圆,连接DE、DA,
∵![]() ,
,![]() ,
,
∴M、A、E、C四点共圆,
∵![]() ,
,![]() ,
,
∴![]() ,∠ABO=45°,
,∠ABO=45°,
∴∠ABG=45°
∵![]() ,
,
∴BG=CG=1,
∴EG=BG=1,
∴点E坐标为(-1,2)
∵![]() ,
,
∴∠MAF+CAH=90°,
∵∠MAF+∠AMF=90°,
∴∠AMF=∠CAH,
∵![]() ,
,
∴△AMF≌△CAH,
∴MF=AH=2,AM=CH=4,
∴点M的坐标为(-7,2),
当点P与点B重合时,点M与点E重合,此时的坐标为(-1,2),
∴当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则点
时,则点![]() 运动的路径长为线段ME的长,ME=-1-(-7)=6,
运动的路径长为线段ME的长,ME=-1-(-7)=6,
故答案为:6.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数(次) | 0 | 1 | 2 | 3 | 4 | 5 |
人数(人) | 11 | 15 | 23 | 28 | 20 | 3 |
(1)这天部分出行学生使用共享单车次数的众数是_________(次).
(2)求这天部分出行学生平均每人使用共享单车的次数.
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
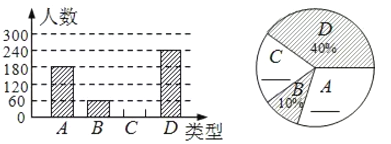
【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |

根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.