题目内容
在菱形ABCD中,∠ABC=60°,AB=1,E为边BC的中点.则对角线BD上的动点P到E、C两点的距离之和的最小值为
- A.
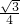
- B.

- C.

- D.

C
分析:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,根据菱形的性质得出OA=0C,AC⊥BD,AB=BC,得到A和C关于BD对称,由∠ABC=60°,得出等边三角形ACB,推出AC=AB,根据等腰三角形的性质推出AE⊥BC,推出∠BAE=30°,求出BE和AE长,即可求出答案.
解答: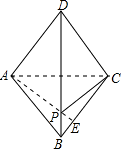 解:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,
解:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,
∵菱形ABCD,
∴OA=0C,AC⊥BD,AB=BC,
A和C关于BD对称,
∴AP=CP,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=1,
∵E为边BC的中点,
∴AE⊥BC,
∴∠BAE=30°,
∴BE= ,
,
根据勾股定理得:AE= ,
,
∴PE+PC=AE= .
.
故选C.
点评:本题主要考查对菱形的性质,等腰三角形的性质,等边三角形的性质和判定,三角形的内角和定理,勾股定理,轴对称,含30度角的直角三角形的性质等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键,此题综合性强,难度适中.
分析:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,根据菱形的性质得出OA=0C,AC⊥BD,AB=BC,得到A和C关于BD对称,由∠ABC=60°,得出等边三角形ACB,推出AC=AB,根据等腰三角形的性质推出AE⊥BC,推出∠BAE=30°,求出BE和AE长,即可求出答案.
解答:
 解:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,
解:连接AC、AE,AE交BD于P,则此时PE+PC最小,连接CP,∵菱形ABCD,
∴OA=0C,AC⊥BD,AB=BC,
A和C关于BD对称,
∴AP=CP,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=1,
∵E为边BC的中点,
∴AE⊥BC,
∴∠BAE=30°,
∴BE=
 ,
,根据勾股定理得:AE=
 ,
,∴PE+PC=AE=
 .
.故选C.
点评:本题主要考查对菱形的性质,等腰三角形的性质,等边三角形的性质和判定,三角形的内角和定理,勾股定理,轴对称,含30度角的直角三角形的性质等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键,此题综合性强,难度适中.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数=
14、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF,则∠CDF的度数=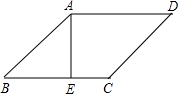 如图,在菱形ABCD中,AE⊥BC于E,已知EC=1,cosB=
如图,在菱形ABCD中,AE⊥BC于E,已知EC=1,cosB=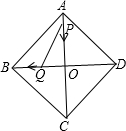 如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.
如图所示,在菱形ABCD中,AC,BD交于点O,AB=15,AO=12,P从A出发,Q从O出发,分别以2cm/s和1cm/s的速度各自向O,B点运动,当运动时间为多少秒时,四边形BQPA的面积是△POQ面积的8倍.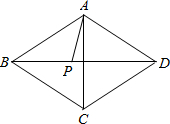 如图,在菱形ABCD中,P为对角线BD上一点,连接AP,若AP=BP,AD=PD,则∠PAC的度数是( )
如图,在菱形ABCD中,P为对角线BD上一点,连接AP,若AP=BP,AD=PD,则∠PAC的度数是( )