题目内容
【题目】如图,矩形ABCD的顶点 A的坐标为(4,2),顶点B,C分别在![]() 轴,
轴,![]() 轴的正半轴上.
轴的正半轴上.
(1)求证:∠OCB=∠ABE;
(2)求OC长的取值范围;
(3)若D的坐标为(![]() ,
,![]() ),请说明
),请说明![]() 随
随![]() 的变化情况.
的变化情况.

【答案】(1)证明见解析;(2)0<OC≤2.(3)当0<![]() ≤2时,
≤2时,![]() 随
随![]() 的增大而增大;当2≤
的增大而增大;当2≤![]() <2时,
<2时,![]() 随
随![]() 的增大而减小.
的增大而减小.
【解析】试题分析:(1)根据矩形的性质得出∠CBA=∠COB=90°,求出∠OCB+∠CBO=90°,∠CBO+∠ABE=90°,即可得出答案;(2)过A作AF⊥x轴于F,证△COB∽△BEA,得出比例式,设OB=x,OC=y,则BE=4﹣x,求出y=﹣x2+2x=﹣![]() (x﹣2)2+2,即可得出答案;(3)求出n=﹣
(x﹣2)2+2,即可得出答案;(3)求出n=﹣![]() (m﹣2)2+4,根据二次函数的性质得出即可.
(m﹣2)2+4,根据二次函数的性质得出即可.
试题解析:
(1)证明:∵矩形ABCD,
∴∠ABC=90°,
∵∠BOC=90°,
∴∠ABC=∠BOC,
∵∠BOC+∠OCB=∠ABC+∠ABE,
∴∠OCB=∠ABE.
(2)解:过点A作AF⊥![]() 轴于F,
轴于F,
当点B在点F时,OC的长最小,为0.
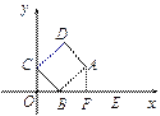
设OB=![]() ,OC=
,OC=![]() ,则BF=4-
,则BF=4-![]() .
.
∵AF⊥![]() 轴,
轴,
∴∠AFB=90°.
∴∠BOC=∠AFB=90°.
∴△BOC∽△AEB.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴OC的最大值为2.
∴OC的取值范围是0<OC≤2.
(3)解:过点D作AH⊥![]() 轴于H.
轴于H.
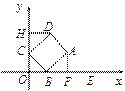
由矩形的性质易得△DHC≌△BFA.
∴DH=BF=4-![]() ,
,
CH=AF=2.
∴![]() ,
,![]() .
.
∴![]() .
.
∵0≤![]() <4,
<4,
∴0<![]() ≤4.
≤4.
∴当0<![]() ≤2时,
≤2时,![]() 随
随![]() 的增大而增大;当2≤
的增大而增大;当2≤![]() <2时,
<2时,![]() 随
随![]() 的增大而减小.
的增大而减小.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】某公园门票的收费标准如下:
门票类别 | 成人票 | 儿童票 | 团体票(限5张及以上) |
价格(元/人) | 100 | 40 | 60 |
有两个家庭分别去该公园游玩,每个家庭都有5名成员,且他们都选择了最省钱的方案购买门票,结果一家比另一家少花40元,则花费较少的一家花了_____元.