题目内容
【题目】(本小题满分11分)学之道在于悟.希望同学们在问题(1)解决过程中有所悟,再继续探索研究问题(2).
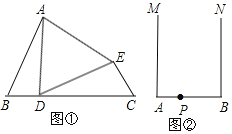
(1)如图①,∠B=∠C,BD=CE,AB=DC.
①求证:△ADE为等腰三角形.
②若∠B=60°,求证:△ADE为等边三角形.
(2)如图②,射线AM与BN,AM⊥AB,BN⊥AB,点P是AB上一点,在射线AM与BN上分别作点C、点D满足:△CPD为等腰直角三角形.(要求:利用直尺与圆规,不写作法,保留作图痕迹)
【答案】见解析
【解析】(1)①在△ABD和△DCE中,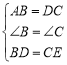 ,
,
∴△ABD≌△DCE(SAS),∴AD=DE,即△ADE为等腰三角形;(2分)
②∵△ABD≌△DCE,∴∠BAD=∠CDE,
∵∠B=60°,∴∠BAD+∠ADB=120°,∴∠CDE+∠ADB=120°,
∴∠ADE=60°,又∵△ADE为等腰三角形,∴△ADE为等边三角形;(5分)
(2)有三种情况,PC=PD、CP=CD、DC=DP,如图所示:
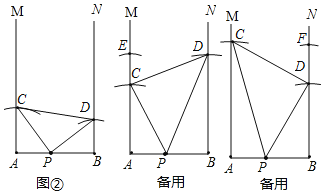 (11分)
(11分)

练习册系列答案
相关题目
