题目内容
已知D在△ABC的边AB上,△ABC∽△ACD,相似比为2,△BDC的面积记作S△BDC,△DAC的面积记作S△DAC,△ABC的面积记作S△ABC,下列命题错误的是
- A.AB:AC=2:1
- B.AD:AB=1:4
- C.S△BDC:S△DAC=3:1
- D.S△BDC:S△ABC=4:3
D
分析:利用相似三角形的相似比就是对应边的比,面积比等于对应边比的平方.
解答:∵△ABC∽△ACD,
∴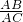 =
=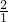 ,
,
∴S△ACD:S△ABC=AD:AB=1:4,
∴S△ACD= S△ABC.
S△ABC.
又∵△ACD的面积与△BCD的面积和等于△ABC的面积,
∴S△BCD= S△ABC∴S△BCD:S△ACD=3:1,
S△ABC∴S△BCD:S△ACD=3:1,
∴S△ABC:S△BDC=4:3.
故选D.
点评:此题运用了三角形的面积比等于相似比的平方,还有同高的三角形的面积比等于底边的比.
分析:利用相似三角形的相似比就是对应边的比,面积比等于对应边比的平方.
解答:∵△ABC∽△ACD,
∴
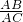 =
=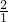 ,
,∴S△ACD:S△ABC=AD:AB=1:4,
∴S△ACD=
 S△ABC.
S△ABC.又∵△ACD的面积与△BCD的面积和等于△ABC的面积,
∴S△BCD=
 S△ABC∴S△BCD:S△ACD=3:1,
S△ABC∴S△BCD:S△ACD=3:1,∴S△ABC:S△BDC=4:3.
故选D.
点评:此题运用了三角形的面积比等于相似比的平方,还有同高的三角形的面积比等于底边的比.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
已知D在△ABC的边AB上,△ABC∽△ACD,相似比为2,△BDC的面积记作S△BDC,△DAC的面积记作S△DAC,△ABC的面积记作S△ABC,下列命题错误的是( )
| A、AB:AC=2:1 | B、AD:AB=1:4 | C、S△BDC:S△DAC=3:1 | D、S△BDC:S△ABC=4:3 |