题目内容
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
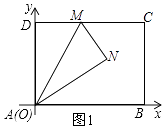
第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图①);
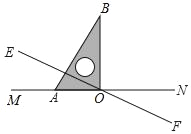
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线BM的解析式为y=kx,求k的值;
(Ⅱ)若MN的延长线与矩形ABCD的边BC交于点P,设矩形的边AB=a,BC=b;
(i)若a=2,b=4,求P点的坐标;
(ii)请直接写出a、b应该满足的条件.
【答案】解:
(Ⅰ)连接AN,延长MN交BC于点P,如图,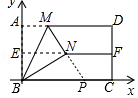
∴EF垂直平分AB,
∴AN=BN,
由折叠知AB=BN,
∴AN=AB=BN,
∴△ABN为等边三角形,
∴∠ABN=60°,
∴∠PBN=30°,
∵∠ABM=∠NBM=30°,
∴∠BNM=∠A=90°,
∴∠BPN=60°,∠MBP=∠MBN+∠PBN=60°,
∴∠BMP=60°,
∴∠MBP=∠BMP=∠BPM=60°,
∴△BMP是等边三角形,
∵点M在直线y=kx上,
∴k= ![]() =tan60°=
=tan60°= ![]() ;
;
(Ⅱ)(i)由题意可知AB=a=2,
在Rt△ABM中,cos∠ABM= ![]() ,
,
∴ ![]() =
= ![]() ,解得BM=
,解得BM= ![]() ,
,
∴BP=BM= ![]() ,
,
∴P( ![]() ,0);
,0);
(ii)由题意可知BC≥BP,
在Rt△BNP中,BN=BA=a,∠PBN=30°,
∴BP= ![]() ,
,
∴b≥ ![]() ,
,
∴a≤ ![]() b
b
【解析】(Ⅰ)连接AN,延长MN交BC于点P,由折叠的性质可证△BMP为等边三角形,由M点的坐标可求得k的值;(Ⅱ)(i)在Rt△ABM中,由三角形的性质可求得BM的长,则可求得BP的长,可求得P点坐标;(ii)由题意可知BC≥BP,在Rt△BNP中,由三角函数的定义可用a表示出BP,则可得到a、b所满足的条件.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.