题目内容
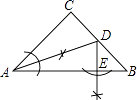
【题目】如图，斜面AC的坡度为1：2，AC=3 
米，坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带相连，若AB=10米，则旗杆BC的高度为（ ） 
A.5米
B.6米
C.8米
D.（3+ ）米
【答案】A
【解析】解：在Rt△ACD中，
∵CD：AD=1：2，
∴设CD=x，AD=2x，
又∵AC=3 
米，
∴x2+4x2=45，
解得：x=3，
则AD=6（米），
∵AB=10米，
∴BD= 
=8（米），
则BC=8﹣3=5（米）．
故选A．
【考点精析】根据题目的已知条件，利用关于坡度坡角问题的相关知识可以得到问题的答案，需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)．用字母i表示，即i=h/l．把坡面与水平面的夹角记作A(叫做坡角)，那么i=h/l=tanA．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
【题目】用描点法画二次函数y=ax2+bx+c(a≠0)的图象时，列出了如下表格：
x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
y=ax2+bx+c(a≠0) | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
那么当该二次函数值y > 0时，x的取值范围是_________.
