题目内容
对关于 的一次函数
的一次函数 和二次函数
和二次函数 .
.
(1) 当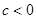 时, 求函数
时, 求函数 的最大值;
的最大值;
(2) 若直线 和抛物线
和抛物线 有且只有一个公共点, 求
有且只有一个公共点, 求
 的值.
的值.
 的一次函数
的一次函数 和二次函数
和二次函数 .
.(1) 当
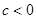 时, 求函数
时, 求函数 的最大值;
的最大值;(2) 若直线
 和抛物线
和抛物线 有且只有一个公共点, 求
有且只有一个公共点, 求 的值.
的值.2013;-6
试题分析:(1) 因为
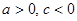 , 所以判别式
, 所以判别式 , 函数
, 函数 和
和 轴必有两个交点,
轴必有两个交点,则函数
 的最小值为0, 则函数
的最小值为0, 则函数 的最大值应为2013;
的最大值应为2013;(2) 将直线与抛物线解析式联立, 消去
 , 得
, 得 , 因为直线与抛物线有且只有一个公共点, 所以判别式等于零, 化简整理成
, 因为直线与抛物线有且只有一个公共点, 所以判别式等于零, 化简整理成 ,
,对于
 取任何实数, 上式恒成立, 所以应有
取任何实数, 上式恒成立, 所以应有 同时成立, 解得
同时成立, 解得 , 所以
, 所以 .
.点评:一元二次方程根的判别式是
 ,当
,当 时,方程有两个不相等的实数根;当
时,方程有两个不相等的实数根;当 时,方程没有实数根,该方程无解;
时,方程没有实数根,该方程无解; 时,该方程有两个相等的实数根。
时,该方程有两个相等的实数根。
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),A点的横坐标为-1.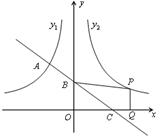
 (x>0)的图象与
(x>0)的图象与 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在 ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与 由直线
由直线 :
: 沿
沿 轴向右平移9个单位得到,则直线
轴向右平移9个单位得到,则直线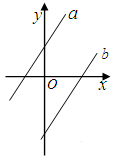
 是正比例函数,则a=___________。
是正比例函数,则a=___________。 分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事相吻合的是( )
分别表示乌龟和兔子所行的路程,t为时间,则下列图像中与故事相吻合的是( )
 与函数
与函数 在同一坐标系中的大致图象是下图中的 ( )
在同一坐标系中的大致图象是下图中的 ( )
 ,其中实数k满足0<k<1,
,其中实数k满足0<k<1,