题目内容
【题目】已知一次函数 y=(m﹣2)x+3﹣m 的图象不经过第三象限,且 m 为正整数.
(1)求 m 的值.
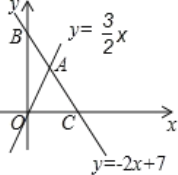
(2)在给出的平面直角坐标系中画出该一次函数的图象.
(3)当﹣4<y<0 时,根据函数图象,求 x 的取值范围.

【答案】(1) m 的值是 1;(2)见解析;(3) 2<x<6.
【解析】
(1)根据一次函数的图象不经过第三象限确定m的不等式组,从而确定m的值;
(2)确定m的值后利用两点法作图即可;
(3)根据图象确定自变量的取值范围即可.
(1)∵一次函数 y=(m﹣2)x+3﹣m 的图象不经过第三象限,
∴![]() ,得 m<2,
,得 m<2,
∵m 为正整数,
∴m=1,
即 m 的值是 1;
(2)由(1)知,m=1,
∴y=(1﹣2)x+3﹣1=﹣x+2,
当 x=0 时,y=2,当 y=0 时,x=2, 该一次函数的图象如右图所示;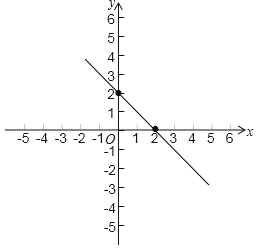
(3)当 y=﹣4 时,﹣4=﹣x+2,得 x=6,当 y=0 时,0=﹣x+2,得 x=2, 由图象可得,当﹣4<y<0 时,x 的取值范围是 2<x<6.

 阅读快车系列答案
阅读快车系列答案【题目】小丽妈妈在网上做淘宝生意,专门销售女式鞋子,一次,小丽发现一个进货单上的一个信息是:A款鞋的进价比B款鞋进价多20元,花500元进A款鞋的数量和花400元进B款鞋的数量相同.
(1)问A、B款鞋的进价分别是多少元?
(2)小丽在销售单上记录了两天的数据如表:
日期 | A款女鞋销量 | B款女鞋销量 | 销售总额 |
6月1日 | 12双 | 8双 | 2240元 |
6月2日 | 8双 | 10双 | 1960元 |
请问两种鞋的销售价分别是多少?
(3)小丽妈妈说:“两款鞋的利润率相同”,请通过计算,结合(1)(2)所给信息,判断小丽妈妈的说法是否正确,如果正确,请说明理由;如果错误,能否只调整其中一款的售价,使得两款鞋的利润率相同?能否同时调整两款的售价,使得两款鞋的利润率相同?请说明理由.