题目内容
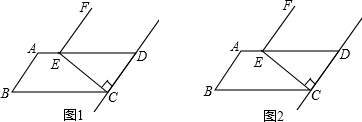
在平行四边形ABCD中,过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90°得到线段EF(如图1)
(1)在图1中画图探究:
①当P为射线CD上任意一点(P1不与C重合)时,连接EP1;绕点E逆时针旋转90°得到线段EG1.判断直线FG1与直线CD的位置关系,并加以证明;
②当P2为线段DC的延长线上任意一点时,连接EP2,将线段EP2绕点E逆时针旋转90°得到线段EG2.判断直线G1G2与直线CD的位置关系,画出图形并直接写出你的结论.
(2)若AD=6,tanB= ,AE=1,在①的条件下,设CP1=x,S△P1FG1=y,求y与x之间的函数关系式,并写出自变量x的取值范围.
,AE=1,在①的条件下,设CP1=x,S△P1FG1=y,求y与x之间的函数关系式,并写出自变量x的取值范围.
 解:(1)①直线FG1与直线CD的位置关系为互相垂直.
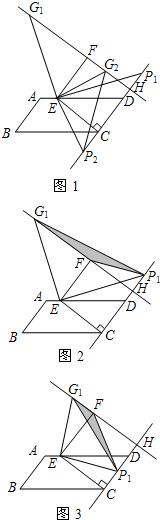
解:(1)①直线FG1与直线CD的位置关系为互相垂直.证明:如图1,设直线FG1与直线CD的交点为H.
∵线段EC、EP1分别绕点E逆时针旋转90°依次得到线段EF、EG1,
∴∠P1EG1=∠CEF=90°,EG1=EP1,EF=EC.
∵∠G1EF=90°-∠P1EF,∠P1EC=90°-∠P1EF,
∴∠G1EF=∠P1EC.
∴△G1EF≌△P1EC.
∴∠G1FE=∠P1CE.
∵EC⊥CD,
∴∠P1CE=90°,
∴∠G1FE=90度.
∴∠EFH=90度.
∴∠FHC=90度.
∴FG1⊥CD.
②按题目要求所画图形见图1,直线G1G2与直线CD的位置关系为互相垂直.
(2)∵四边形ABCD是平行四边形,
∴∠B=∠ADC.
∵AD=6,AE=1,tanB=
 ,
,∴DE=5,tan∠EDC=tanB=
 .
.可得CE=4.
由(1)可得四边形EFHC为正方形.
∴CH=CE=4.
①如图2,当P1点在线段CH的延长线上时,
∵FG1=CP1=x,P1H=x-4,
∴S△P1FG1=
 ×FG1×P1H=
×FG1×P1H=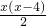 .
.∴y=
 x2-2x(x>4).
x2-2x(x>4).②如图3,当P1点在线段CH上(不与C、H两点重合)时,
∵FG1=CP1=x,P1H=4-x,
∴S△P1FG1=
 ×FG1×P1H=
×FG1×P1H=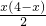 .
.∴y=-
 x2+2x(0<x<4).
x2+2x(0<x<4).③当P1点与H点重合时,即x=4时,△P1FG1不存在.
综上所述,y与x之间的函数关系式及自变量x的取值范围是y=
 x2-2x(x>4)或y=-
x2-2x(x>4)或y=- x2+2x(0<x<4).
x2+2x(0<x<4).分析:(1)①直线FG1与直线CD的位置关系为互相垂直,理由为:△P1EC按要求旋转后得到的△G1EF全等,再结合∠P1CE=∠G1FE=90°去说明;②按题目要求所画图形见图1,直线G1G2与直线CD的位置关系为互相垂直;
(2)①当点P1在线段CH的延长线上时,结合已知说明CE=4,且由四边形FEHC是正方形,得CH=CE=4,再根据题设可得G1F=x.P1H=x-4,进而可得y与x之间的函数关系式;②当点P1在线段CH上时,同理可得FG1=x,P1H=4-x,进而可得y与x之间的函数关系式;③当点P1与点H重合时,说明△P1FG1不存在,再作综合说明即可.
点评:本题着重考查了二次函数解、图形旋转变换、三角形全等、探究垂直的构成情况等重要知识点,综合性强,能力要求较高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
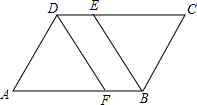 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F.试判断AF与CE是否相等,并说明理由. 24、已知如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形.
24、已知如图,在平行四边形ABCD中,BN=DM,BE=DF.求证:四边形MENF是平行四边形. (2013•鞍山一模)在平行四边形ABCD中,∠DAB=60°,点E是AD的中点,点O是AB边上一点,且AO=AE,过点E作直线HF交DC于点H,交BA的延长线于F,以OE所在直线为对称轴,△FEO经轴对称变换后得到△F′EO,直线EF′交直线DC于点M.
(2013•鞍山一模)在平行四边形ABCD中,∠DAB=60°,点E是AD的中点,点O是AB边上一点,且AO=AE,过点E作直线HF交DC于点H,交BA的延长线于F,以OE所在直线为对称轴,△FEO经轴对称变换后得到△F′EO,直线EF′交直线DC于点M. 如图,在平行四边形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F.求证:BE=DF.
如图,在平行四边形ABCD中,AE⊥AD交BD于点E,CF⊥BC交BD于点F.求证:BE=DF. 如图,在平行四边形ABCD中,∠B的平分线交AD于E,AE=10,ED=4,那么平行四边形ABCD的周长是
如图,在平行四边形ABCD中,∠B的平分线交AD于E,AE=10,ED=4,那么平行四边形ABCD的周长是