题目内容
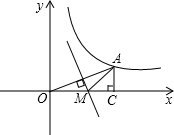（2012•漳州）如图，点A（3，n）在双曲线y=| 3 | x |
4
4
．分析：先求出点A的坐标，根据点的坐标的定义得到OC=3，AC=1，再根据线段垂直平分线的性质可知AM=OM，由此推出△AMC的周长=OC+AC．
解答：解：∵点A（3，n）在双曲线y=
上，
∴n=
=1，∴A（3，1），
∴OC=3，AC=1．
∵OA的垂直平分线交OC于M，
∴AM=OM，
∴△AMC的周长=AM+MC+AC=OM+MC+AC=OC+AC=3+1=4．
故答案为4．
| 3 |
| x |
∴n=
| 3 |
| 3 |
∴OC=3，AC=1．
∵OA的垂直平分线交OC于M，
∴AM=OM，
∴△AMC的周长=AM+MC+AC=OM+MC+AC=OC+AC=3+1=4．
故答案为4．
点评：本题主要考查了反比例函数的图象性质和线段中垂线的性质，将求△AMC的周长转换成求OC+AC是解题的关键．
练习册系列答案
相关题目
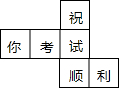（2012•漳州）如图，是一个正方体的平面展开图，原正方体中“祝”的对面是（ ）
（2012•漳州）如图，在等腰梯形ABCD中，AD∥BC，AB=DC，∠B=80°，则∠D的度数是（ ）
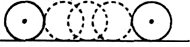（2012•漳州）如图，一枚直径为4cm的圆形古钱币沿着直线滚动一周，圆心移动的距离是（ ）
（2012•漳州）如图，⊙O的半径为3cm，当圆心0到直线AB的距离为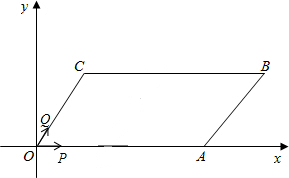
（2012•漳州）如图，在?OABC中，点A在x轴上，∠AOC=60°，0C=4cm．OA=8cm．动点P从点O出发，以1cm/s的速度沿线段OA→AB运动；动点Q同时从点O出发，以acm/s的速度沿线段OC→CB运动，其中一点先到达终点B时，另一点也随之停止运动．设运动时间为t秒．