题目内容
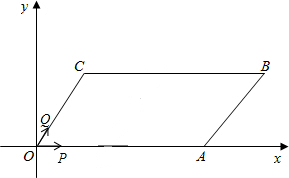 (2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.
(2012•漳州)如图,在?OABC中,点A在x轴上,∠AOC=60°,0C=4cm.OA=8cm.动点P从点O出发,以1cm/s的速度沿线段OA→AB运动;动点Q同时从点O出发,以acm/s的速度沿线段OC→CB运动,其中一点先到达终点B时,另一点也随之停止运动.设运动时间为t秒.(1)填空:点C的坐标是(
2
2
,2
| 3 |
2
),对角线OB的长度是| 3 |
4
| 7 |
4
cm;| 7 |
(2)当a=1时,设△OPQ的面积为S,求S与t的函数关系式,并直接写出当t为何值时,S的值最大?
(3)当点P在OA边上,点Q在CB边上时,线段PQ与对角线OB交于点M.若以O、M、P为顶点的三角形与△OAB相似,求a与t的函数关系式,并直接写出t的取值范围.
分析:(1)首先过点C作CD⊥OA于D,过点B作BE⊥OA于E,连接OB,由∠AOC=60°,0C=4cm,利用三角函数求得OD与CD的长,即可得点C的坐标;又由四边形OABC是平行四边形,可得BE与AB的长,继而求得AE的长,然后由勾股定理,即可求得对角线OB的长度;
(2)分别从当0<t≤4时,当4≤t≤8时与当8≤t≤12时去分析求解即可求得答案;
(3)分别从当△OPM∽△OAB与当△OPM∽△OBA时去分析,利用相似三角形的对应边成比例,即可求得答案.
(2)分别从当0<t≤4时,当4≤t≤8时与当8≤t≤12时去分析求解即可求得答案;
(3)分别从当△OPM∽△OAB与当△OPM∽△OBA时去分析,利用相似三角形的对应边成比例,即可求得答案.
解答: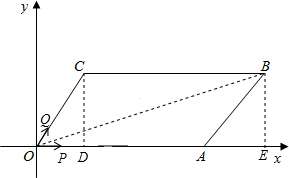 解:(1)过点C作CD⊥OA于D,过点B作BE⊥OA于E,连接OB,
解:(1)过点C作CD⊥OA于D,过点B作BE⊥OA于E,连接OB,
∵∠AOC=60°,0C=4cm,
∴OD=0C•cos60°=4×
=2(cm),CD=OC•sin60°=4×
=2
(cm),
∴C(2,2
),
∵四边形OABC是平行四边形,
∴AB=OC=4cm,BC∥OA,
∴BE=CD=2
cm,
∴AE=
=2(cm),
∵OA=8cm,
∴OE=OA+AE=10(cm),
∴OB=
=4
cm.…(4分)
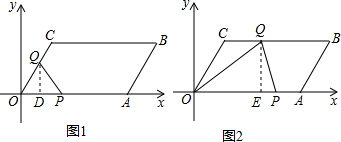 (2)①当0<t≤4时,
(2)①当0<t≤4时,
过点Q作QD⊥x轴于点D(如图1),则QD=
t.
∴S=
OP•QD=
t2.…(5分)
②当4≤t≤8时,
作QE⊥x轴于点E(如图2),则QE=2
.
∴S=
OP•QE=
t. …(6分)
③当8≤t<12时,
解法一:延长QP交x轴于点F,过点P作PH⊥AF于点H(如图3).
∴△PBQ与△PAF均为等边三角形,
∴OF=OA+AP=t,AP=t-8.
∴PH=
(t-8).…(7分)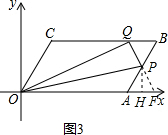
∴S=S△OQF-S△OPF
=
t•2
-
t•
(t-8)
=-
t2+3
t. …(8分)
当t=8时,S最大. …(9分)
解法二:过点P作PH⊥x轴于点H(如图3).
∴△PBQ为等边三角形.
∵AP=t-8.
∴PH=
(t-8). …(7分)
∴S=S梯形OABQ-S△PBQ-S△OAP=
(20-t)-
(12-t)2-2
(t-8).
=-
t2+3
t. …(8分)
当t=8时,S最大. …(9分)
(3)①当△OPM∽△OAB时(如图4),则PQ∥AB.
∴CQ=OP.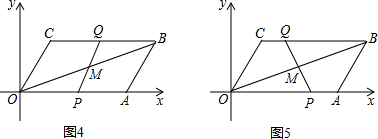
∴at-4=t,a=1+
.…(10分)
t的取值范围是0<t<8. …(11分)
②当△OPM∽△OBA时(如图5),
则
=
,
∴
=
,
∴OM=
t. …(12分)
又∵QB∥OP,
∴△BQM∽△OPM,
∴
=
,
∴
=
,
整理得t-at=2,
∴a=1-
.…(13分)
t的取值范围是6≤t≤8.
综上所述:a=1+
(0<t<8)或a=1-
(6≤t≤8). …(14分)
 解:(1)过点C作CD⊥OA于D,过点B作BE⊥OA于E,连接OB,
解:(1)过点C作CD⊥OA于D,过点B作BE⊥OA于E,连接OB,∵∠AOC=60°,0C=4cm,
∴OD=0C•cos60°=4×
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴C(2,2
| 3 |
∵四边形OABC是平行四边形,
∴AB=OC=4cm,BC∥OA,
∴BE=CD=2
| 3 |
∴AE=
| AB2-BE2 |
∵OA=8cm,
∴OE=OA+AE=10(cm),
∴OB=
| OE2+BE2 |
| 7 |
 (2)①当0<t≤4时,
(2)①当0<t≤4时,过点Q作QD⊥x轴于点D(如图1),则QD=
| ||
| 2 |
∴S=
| 1 |
| 2 |
| ||
| 4 |
②当4≤t≤8时,
作QE⊥x轴于点E(如图2),则QE=2
| 3 |
∴S=
| 1 |
| 2 |
| 3 |
③当8≤t<12时,
解法一:延长QP交x轴于点F,过点P作PH⊥AF于点H(如图3).
∴△PBQ与△PAF均为等边三角形,
∴OF=OA+AP=t,AP=t-8.
∴PH=
| ||
| 2 |

∴S=S△OQF-S△OPF
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
=-
| ||
| 4 |
| 3 |
当t=8时,S最大. …(9分)
解法二:过点P作PH⊥x轴于点H(如图3).
∴△PBQ为等边三角形.
∵AP=t-8.
∴PH=
| ||
| 2 |
∴S=S梯形OABQ-S△PBQ-S△OAP=
| 3 |
| ||
| 4 |
| 3 |
=-
| ||
| 4 |
| 3 |
当t=8时,S最大. …(9分)
(3)①当△OPM∽△OAB时(如图4),则PQ∥AB.
∴CQ=OP.
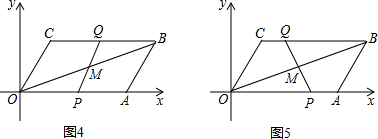
∴at-4=t,a=1+
| 4 |
| t |
t的取值范围是0<t<8. …(11分)
②当△OPM∽△OBA时(如图5),
则
| OP |
| OB |
| OM |
| OA |
∴
| t | ||
4
|
| OM |
| 8 |
∴OM=
2
| ||
| 7 |
又∵QB∥OP,
∴△BQM∽△OPM,
∴
| QB |
| OP |
| BM |
| OM |
∴
| 12-at |
| t |
4
| ||||||
|
整理得t-at=2,
∴a=1-
| 2 |
| t |
t的取值范围是6≤t≤8.
综上所述:a=1+
| 4 |
| t |
| 2 |
| t |
点评:此题考查了相似三角形的判定与性质、平行四边形的性质、直角三角形的性质、勾股定理三角函数、二次函数的最值以及三角形面积问题.此题综合性很强,难度较大,解题的关键是掌握辅助线的作法,注意数形结合思想、分类讨论思想与函数思想的应用.

练习册系列答案
相关题目
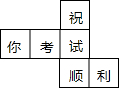 (2012•漳州)如图,是一个正方体的平面展开图,原正方体中“祝”的对面是( )
(2012•漳州)如图,是一个正方体的平面展开图,原正方体中“祝”的对面是( ) (2012•漳州)如图,在等腰梯形ABCD中,AD∥BC,AB=DC,∠B=80°,则∠D的度数是( )
(2012•漳州)如图,在等腰梯形ABCD中,AD∥BC,AB=DC,∠B=80°,则∠D的度数是( )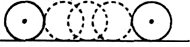 (2012•漳州)如图,一枚直径为4cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是( )
(2012•漳州)如图,一枚直径为4cm的圆形古钱币沿着直线滚动一周,圆心移动的距离是( ) (2012•漳州)如图,⊙O的半径为3cm,当圆心0到直线AB的距离为
(2012•漳州)如图,⊙O的半径为3cm,当圆心0到直线AB的距离为