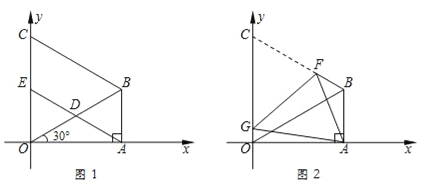
��Ŀ����
����Ŀ��ֱ��y=�� ![]() x+4��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
x+4��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
����ֱ��д����C����D�����꣬�����m��ֵ��
�ڵ�P��0��t�����߶�OB�ϵ�һ�����㣨��P����0��B�غϣ���
������P��ƽ����x���ֱ�߽�AB��M����CE��N�����߶�MN�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д�Ա�����ȡֵ��Χ����
�۵�t=2ʱ���߶�MN��BC��AE֮����ʲô��ϵ����д�����̣�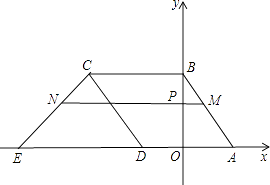
���𰸡��⣺�١�ֱ��y=�� ![]() x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��
x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��
���A��������3��0����B��������0��4����
���ı���ABCD�����Σ�
��ֱ��y=x+m������C��
��m=9��
�ڡ�MN ������P��0��t����ƽ����x�ᣬ
������M��������xM �� t������N��������xN �� t����
�ߵ�M��ֱ��AB�ϣ�
ֱ��AB�Ľ���ʽΪy=�� ![]() x+4��
x+4��
��t=�� ![]() xM+4����xM=��
xM+4����xM=�� ![]() t+3��
t+3��
ͬ����N��ֱ��CE�ϣ�ֱ��CE�Ľ���ʽΪy=x+9��
��t=xN+9����xN=t��9��
��MN��x�����߶�MN�ij���Ϊd��
��d=xM��xN=�� ![]() t+3����t��9��=��
t+3����t��9��=�� ![]() t+12��0��t��4��
t+12��0��t��4��
��MN= ![]() ��BC+AE����
��BC+AE����
���ɣ���t=2ʱ��P��0��2����
��OP=2��
��OB=4��
���P��OB�е㣬
��MN��x�ᣬ
��MN������ABCE����λ�ߣ�
��MN= ![]() ��BC+AE����
��BC+AE����
������������ֱ�ߵĽ���ʽ�����A��B������꣬�ٸ������ε����ʼ��������C����D�����꣬�ѵ�C���������ֱ��y=x+m�������m��ֵ�������M������Ϊ��xM �� t������N������Ϊ��xN �� t�����������xM=�� ![]() t+3�������xN=t��9�������õ�d=xM��xN=��
t+3�������xN=t��9�������õ�d=xM��xN=�� ![]() t+3����t��9��=��
t+3����t��9��=�� ![]() t+12�����������P�����꣬�����ó���P��OB�е㣬���ɵó�MN������ABCE����λ���ɵó����ۣ�
t+12�����������P�����꣬�����ó���P��OB�е㣬���ɵó�MN������ABCE����λ���ɵó����ۣ�

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�����Ŀ�����κ���y=ax2+bx+c��a��0��ͼ���ϲ��ֵ�����꣨x��y����Ӧֵ�б����£�
x | �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
y | �� | ��3 | ��2 | ��3 | ��6 | ��11 | �� |
��ú���ͼ��ĶԳ����ǣ� ��
A.ֱ��x=��3
B.ֱ��x=��2
C.ֱ��x=��1
D.ֱ��x=0