题目内容
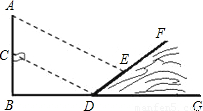
如图，在一旗杆AB上系一活动旗帜C，在某一时刻，旗杆的影子落在平地BD和一坡度为1：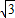
的斜坡DF上，拉动旗帜使其影子正好落在斜坡顶点D处，若测得旗高BC=4m，影长BD=8m，影长DE=6m，（假设旗杆AB与地面垂直，B、D、G三点共线，AB、BG、DF在同一平面内）．（1）求坡角∠FDG的度数；
（2）求旗杆AB的高度． （结果精确到0.1m）
【答案】分析：（1）作EH⊥DG于H，根据坡度为1：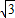
，可得∠FDG=30°；
（2）求出BG的值，根据BC=4m，影长BD=8m，可求得AB的值．
解答：
解：（1）作EH⊥DG于H．
∴tan∠FDG=1：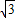
=
．
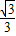∴∠FDG=30°；
（2）∵∠FDG=30°，DE=6m．
∴EH=3m，DH=3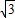
m．
又∵BC=4m，影长BD=8m．
∴HG=6m．
∴BG=BD+DH+HG=8+3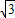
+6=14+3
．
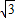∴AB=（14+3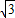
）÷2≈9.6m．
点评：此题主要是运用所学的解直角三角形的知识解决实际生活中的问题．注意：在同一时刻的物高与水平地面上的影长成正比例．
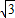，可得∠FDG=30°；（2）求出BG的值，根据BC=4m，影长BD=8m，可求得AB的值．
解答：
解：（1）作EH⊥DG于H．∴tan∠FDG=1：
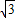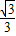=．∴∠FDG=30°；
（2）∵∠FDG=30°，DE=6m．
∴EH=3m，DH=3
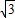m．又∵BC=4m，影长BD=8m．
∴HG=6m．
∴BG=BD+DH+HG=8+3
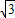+6=14+3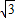．∴AB=（14+3
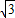）÷2≈9.6m．点评：此题主要是运用所学的解直角三角形的知识解决实际生活中的问题．注意：在同一时刻的物高与水平地面上的影长成正比例．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
、BG、DF在同一平面内）．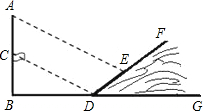
如图，在一旗杆AB上系一活动旗帜C，在某一时刻，旗杆的影子落在平地BD和一坡度为1：
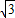的斜坡DF上，拉动旗帜使其影子正好落在斜坡顶点D处，若测得旗高BC=4m，影长BD=8m，影长DE=6m，（假设旗杆AB与地面垂直，B、D、G三点共线，AB、BG、DF在同一平面内）．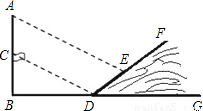
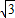的斜坡DF上，拉动旗帜使其影子正好落在斜坡顶点D处，若测得旗高BC=4m，影长BD=8m，影长DE=6m，（假设旗杆AB与地面垂直，B、D、G三点共线，AB、BG、DF在同一平面内）．