题目内容
【题目】如图，直线AB∥CD，AE平分∠CAB．AE与CD相交于点E，∠ACD=40°，则∠BAE的度数是（ ）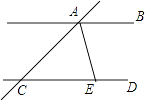 
A.40°
B.70°
C.80°
D.140°
【答案】B
【解析】解：∵AB∥CD， ∴∠ACD+∠BAC=180°，
∵∠ACD=40°，
∴∠BAC=180°﹣40°=140°，
∵AE平分∠CAB，
∴∠BAE= 
∠BAC= ×140°=70°，
故选B．
先由平行线性质得出∠ACD与∠BAC互补，并根据已知∠ACD=40°计算出∠BAC的度数，再根据角平分线性质求出∠BAE的度数．本题考查了平行线的性质和角平分线的定义，比较简单；做好本题要熟练掌握两直线平行①内错角相等，②同位角相等，③同旁内角互补；并会书写角平分线定义的三种表达式：若AP平分∠BAC，则①∠BAP=∠PAC，②∠BAP= ∠BAC，③∠BAC=2∠BAP．
阅读快车系列答案
【题目】目前“自驾游”已成为人们出游的重要方式．“五一”节，林老师驾轿车从舟山出发，上高速公路途经舟山跨海大桥和杭州湾跨海大桥到嘉兴下高速，其间用了4.5小时；返回时平均速度提高了10千米/小时，比去时少用了半小时回到舟山．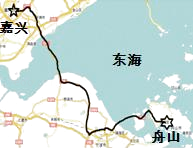 
（1）求舟山与嘉兴两地间的高速公路路程；
（2）两座跨海大桥的长度及过桥费见下表：
大桥名称 | 舟山跨海大桥 | 杭州湾跨海大桥 |
大桥长度 | 48千米 | 36千米 |
过桥费 | 100元 | 80元 |
我省交通部门规定：轿车的高速公路通行费y（元）的计算方法为：y=ax+b+5，其中a（元/千米）为高速公路里程费，x（千米）为高速公路里程（不包括跨海大桥长），b（元）为跨海大桥过桥费．若林老师从舟山到嘉兴所花的高速公路通行费为295.4元，求轿车的高速公路里程费a．
【题目】为了解某小区某月家庭用水量的情况，从该小区随机抽取部分家庭进行调查，以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0＜x≤6.5 | 13 |
C | 6.5＜x≤9.0 | |
D | 9.0＜x≤11.5 | |
E | 11.5＜x≤14.0 | 6 |
F | x＞4.0 | 3 |
根据以上信息，解答下列问题
（1）家庭用水量在4.0＜x≤6.5范围内的家庭有户，在6.5＜x≤9.0范围内的家庭数占被调查家庭数的百分比是%；
（2）本次调查的家庭数为户，家庭用水量在9.0＜x≤11.5范围内的家庭数占被调查家庭数的百分比是%；
（3）家庭用水量的中位数落在组；
（4）若该小区共有200户家庭，请估计该月用水量不超过9.0吨的家庭数．
