题目内容
【题目】如图,已知二次函数![]() 的图象抛物线与
的图象抛物线与![]() 轴相交于不同的两点
轴相交于不同的两点![]() ,
,![]() ,且
,且![]() ,
,
(1)若抛物线的对称轴为![]() 求的
求的![]() 值;
值;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
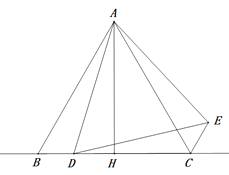
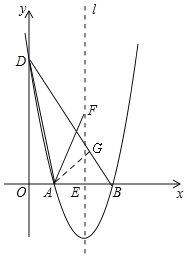
(3)若该抛物线与![]() 轴相交于点D,连接BD,且∠OBD=60°,抛物线的对称轴
轴相交于点D,连接BD,且∠OBD=60°,抛物线的对称轴![]() 与
与![]() 轴相交点E,点F是直线
轴相交点E,点F是直线![]() 上的一点,点F的纵坐标为
上的一点,点F的纵坐标为![]() ,连接AF,满足∠ADB=∠AFE,求该二次函数的解析式.
,连接AF,满足∠ADB=∠AFE,求该二次函数的解析式.

【答案】(1)![]() ;(2)c<
;(2)c<![]() ;(3)
;(3)![]()
【解析】(1)根据抛物线的对称轴公式代入可得a的值;
(2)根据已知得:抛物线与x轴有两个交点,则△>0,列不等式可得c的取值范围;
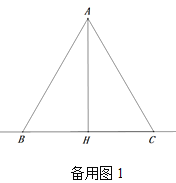
(3)根据60°的正切表示点B的坐标,把点B的坐标代入抛物线的解析式中得:ac=12,则c=![]() ,从而得A和B的坐标,表示F的坐标,作辅助线,构建直角△ADG,根据已知的角相等可得△ADG∽△AFE,列比例式得方程可得a和c的值.
,从而得A和B的坐标,表示F的坐标,作辅助线,构建直角△ADG,根据已知的角相等可得△ADG∽△AFE,列比例式得方程可得a和c的值.
(1)抛物线的对称轴是:x=![]() ,解得:a=
,解得:a=![]() ;
;
(2)由题意得二次函数解析式为:y=15x2-5![]() x+c,
x+c,
∵二次函数与x轴有两个交点,
∴△>0,
∴△=b2-4ac=(5![]() )2-4×15c,
)2-4×15c,
∴c<![]() ;
;
(3)∵∠BOD=90°,∠DBO=60°,
∴tan60°=![]() ,
,
∴OB=![]() ,
,
∴B(![]() ,0),
,0),
把B(![]() ,0)代入y=ax2-5
,0)代入y=ax2-5![]() x+c中得:
x+c中得:![]() ,
,
![]()
∵c≠0,
∴ac=12,
∴c=![]() ,
,
把c=![]() 代入y=ax2-5
代入y=ax2-5![]() x+c中得:
x+c中得:![]()
∴![]()
∴![]()
∴AB=![]() =
=![]() ,AE=
,AE=![]() ,
,
∵F的纵坐标为![]()
∴![]() ,
,
过点A作AG⊥DB于G,
∴BG=![]() AB=AE=
AB=AE=![]() ,AG=
,AG=![]() ,
,
DG=DB-BG=![]() -
-![]() =
=![]() ,
,
∵∠ADB=∠AFE,∠AGD=∠FEA=90°,
∴△ADG∽△AFE,
∴![]() ,
,
∴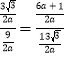
∴![]()
∴![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目