题目内容
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA、OC是方程
=
的两个根(OA>OC),在AB边上取一点D,将纸片沿CD翻折,使点B恰好落在OA边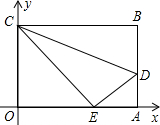 上的点E处.
上的点E处.
(1)求OA、OC的长;
(2)求D、E两点的坐标;
(3)若线段CE上有一动点P自C点沿CE方向向E点匀速运动(点P运动到点E后停止运动),运动的速度为每秒1个单位长度,设运动的时间为t秒,过P点作ED的平行线交CD于点M.是否存在这样的t 值,使以C、E、M为顶点的三角形为等腰三角形?若存在,请直接写出t值及相应的时刻点M的坐标;若不存在,请说明理由.
| 2 |
| x |
| 9-x |
| 10 |
 上的点E处.
上的点E处.(1)求OA、OC的长;
(2)求D、E两点的坐标;
(3)若线段CE上有一动点P自C点沿CE方向向E点匀速运动(点P运动到点E后停止运动),运动的速度为每秒1个单位长度,设运动的时间为t秒,过P点作ED的平行线交CD于点M.是否存在这样的t 值,使以C、E、M为顶点的三角形为等腰三角形?若存在,请直接写出t值及相应的时刻点M的坐标;若不存在,请说明理由.
分析:(1)先根据OA、OC是方程
=
的两个根(OA>OC)即可得出OA、OC的长;
(2)由(1)知OA=5,OC=4,再根据图形翻折变换的性质得出CE=BC=5,∠CED=∠B=90°,DE=BD,Rt△OCE中利用勾股定理即可求出OE的长,进而得出E点坐标,设BD=x,则AD=4-x,DE=x,在Rt△ADE中利用勾股定理求出x的值,故可得出D点坐标;
(3)当CM=ME时,由三角形的中位线定理可得出点P是CE的中点,故可得出M点的坐标及t的值;当CM=CE时,过点M作MF⊥BC于点F,交x轴于点E,先由两点间的距离公式求出CD的长,由相似三角形的判定定理得出△CMF∽△CDB,故可得出MF、CF的长,由此得出M点的坐标,再根据△CPM∽△CED可得出CP的长,进而得出t的值.
| 2 |
| x |
| 9-x |
| 10 |
(2)由(1)知OA=5,OC=4,再根据图形翻折变换的性质得出CE=BC=5,∠CED=∠B=90°,DE=BD,Rt△OCE中利用勾股定理即可求出OE的长,进而得出E点坐标,设BD=x,则AD=4-x,DE=x,在Rt△ADE中利用勾股定理求出x的值,故可得出D点坐标;
(3)当CM=ME时,由三角形的中位线定理可得出点P是CE的中点,故可得出M点的坐标及t的值;当CM=CE时,过点M作MF⊥BC于点F,交x轴于点E,先由两点间的距离公式求出CD的长,由相似三角形的判定定理得出△CMF∽△CDB,故可得出MF、CF的长,由此得出M点的坐标,再根据△CPM∽△CED可得出CP的长,进而得出t的值.
解答:解:(1)∵解方程
=
得,x1=4,x2=5,
经检验x1=4,x2=5均是原方程的解,
∵OA>OC,
∴OA=5,OC=4;
(2)∵由(1)知OA=5,OC=4,
∴BC=OA=5,AB=OC=4,
∵△CED由△CBD翻折而成,
∴CE=BC=5,∠CED=∠B=90°,DE=BD,
在Rt△OCE中,
∵OC=4,CE=5,
∴OE=
=
=3,
∴E(3,0);
∴AE=OA-OE=5-3=2,
设BD=x,则AD=4-x,DE=x,
在Rt△ADE中,DE2=AD2+AE2,即x2=(4-x)2+22,解得x=
,
∴AD=4-
=
,
∴D(5,
);
(3)如图1,当CM=ME时,
∵MP∥DE,∠CED=90°,
∴MP⊥CE,
∴点P是CE的中点,
∴t=PC=
CE=
×5=
;
∴PM是△CED的中位线,
∴M是CD的中点,
∵C(0,4),D(5,
),
∴M(
,
);
如图2,当CM=CE时,
过点M作MF⊥BC于点F,交x轴于点E,
∵C(0,4),D(5,
)
∴CD=
=
,
∵MF⊥BC,AB⊥BC,
∴△CMF∽△CDB,
∴
=
=
,即MF=
=
=
,CF=
=
=
,
∴ME=4-MF=4-
,
∴M(
,4-
),
∵PM∥DE,
∴△CPM∽△CED,
∴
=
,即CP=
=
=
,
∴t=CP=
.
| 2 |
| x |
| 9-x |
| 10 |
经检验x1=4,x2=5均是原方程的解,
∵OA>OC,
∴OA=5,OC=4;
(2)∵由(1)知OA=5,OC=4,
∴BC=OA=5,AB=OC=4,
∵△CED由△CBD翻折而成,
∴CE=BC=5,∠CED=∠B=90°,DE=BD,
在Rt△OCE中,
∵OC=4,CE=5,
∴OE=
| CE2-OC2 |
| 52-42 |
∴E(3,0);
∴AE=OA-OE=5-3=2,
设BD=x,则AD=4-x,DE=x,
在Rt△ADE中,DE2=AD2+AE2,即x2=(4-x)2+22,解得x=
| 5 |
| 2 |
∴AD=4-
| 5 |
| 2 |
| 3 |
| 2 |
∴D(5,
| 3 |
| 2 |
(3)如图1,当CM=ME时,

∵MP∥DE,∠CED=90°,
∴MP⊥CE,
∴点P是CE的中点,
∴t=PC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴PM是△CED的中位线,
∴M是CD的中点,
∵C(0,4),D(5,
| 3 |
| 2 |
∴M(
| 5 |
| 2 |
| 11 |
| 4 |
如图2,当CM=CE时,
过点M作MF⊥BC于点F,交x轴于点E,

∵C(0,4),D(5,
| 3 |
| 2 |
∴CD=
52+(4-
|
5
| ||
| 2 |
∵MF⊥BC,AB⊥BC,
∴△CMF∽△CDB,
∴
| CM |
| CD |
| MF |
| BD |
| CF |
| BC |
| CM•BD |
| CD |
5×
| ||||
|
5
| ||
| 3 |
| CM•BC |
| CD |
| 5×5 | ||||
|
10
| ||
| 3 |
∴ME=4-MF=4-
5
| ||
| 3 |
∴M(
10
| ||
| 3 |
5
| ||
| 3 |
∵PM∥DE,
∴△CPM∽△CED,
∴
| CP |
| CE |
| CM |
| CD |
| CE•CM |
| CD |
| 5×5 | ||||
|
10
| ||
| 3 |
∴t=CP=
10
| ||
| 3 |
点评:本题考查的是相似形综合题,涉及到解分式方程、勾股定理、等腰三角形的判定与性质、相似三角形的判定与性质及矩形的性质,先根据题意得出OA、OC的长是解答此题的关键.

练习册系列答案
相关题目
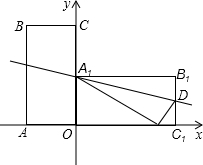
 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标. 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,