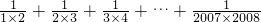Question

在有理数运算时，我们发现了：

1

1×2

=1-

1

2

，

1

2×3

=

1

2

-

1

3

，

1

3×4

=

1

3

-

1

4

…据上述理论，请你计算：
（1）

1

1×2

+

1

2×3

+

1

3×4

+…+

1

2007×2008

（2）

1

1×3

+

1

3×5

+

1

5×7

+…+

1

49×51

Answer 1

分析：（1）分子为1，分母是两个连续自然数的乘积，第n项为

1

n×(n+1)

= 

1

n

- 

1

n+1

，所以原式=1-

1

2

+

1

2

-

1

3

+ 

1

3

-

1

4

+…

1

2007

- 

1

2008

=1-

1

2008

=

2007

2008

．
（2）分子为1，分母是两个连续奇数的乘积，第n项为

1

n×(2n-1)

= 

1

2

( 

1

n

- 

1

2n-1

)，所以原式=

1

2

（1-

1

3

+ 

1

3

- 

1

5

+…+

1

49

- 

1

51

）=

1

2

（1-

1

51

）=

25

51

．

解答：解：（1）

1

1×2

+

1

2×3

+

1

3×4

+…+

1

2007×2008

=1-

1

2

+

1

2

-

1

3

+ 

1

3

-

1

4

+…

1

2007

- 

1

2008

=1-

1

2008

=

2007

2008

；

（2）

1

1×3

+

1

3×5

+

1

5×7

+…+

1

49×51

=

1

2

（1-

1

3

+ 

1

3

- 

1

5

+…+

1

49

- 

1

51

）
=

1

2

（1-

1

51

）
=

25

51

．

点评：解决这类题目找出变化规律，消去中间项，只剩首末两项，使运算变得简单．