题目内容
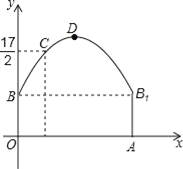
【题目】如图,点B(3,3)在双曲线y=![]() (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣![]() (x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(1)求k的值;
(2)求点A的坐标.

【答案】(1)9.(2)(1,0).
【解析】试题分析:(1)、将点B代入反比例函数解析式求出k的值;(2)、设MD=a,OM=b,从而得出ab=4,过D作DM⊥x轴于M,过B作BN⊥x轴于N,则∠DMA=∠ANB=90°,根据正方形的性质得出△ADM和△BAN全等,从而得出BN=AM=3,DM=AN=a,0A=3﹣a,即AM=b+3﹣a=3,a=b,根据ab=4得出a=b=2,从而得出OA=1,从而求出点A的坐标.
试题解析:(1)、∵点B(3,3)在双曲线y=![]() 上,∴k=3×3=9;
上,∴k=3×3=9;
(2)、∵B(3,3),∴BN=ON=3,设MD=a,OM=b,∵D在双曲线y=![]() (x<0)上,∴ab=4
(x<0)上,∴ab=4
过D作DM⊥x轴于M,过B作BN⊥x轴于N,则∠DMA=∠ANB=90°
∵四边形ABCD是正方形,∴∠DAB=90°,AD="AB" ∴∠MDA+∠DAM=90°,∠DAM+∠BAN=90°,∴∠ADM=∠BAN
在△ADM和△BAN中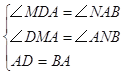 ∴△ADM≌△BAN ∴BN=AM=3,DM=AN=a,∴0A=3﹣a,
∴△ADM≌△BAN ∴BN=AM=3,DM=AN=a,∴0A=3﹣a,
即AM=b+3﹣a=3,a=b, ∵ab=4,∴a=b=2,∴OA=3﹣2=1, 即点A的坐标是(1,0)

练习册系列答案
相关题目