题目内容
如下图,在平面直角坐标系中,点O为坐标原点,以点A(0,-3)为圆心,5为半径作圆A,交x轴于B、C两点,交y轴于点D、E两点.
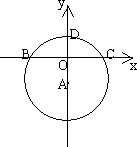
(1)求点B、C、D的坐标;
(2)如果一个二次函数图像经过B、C、D三点,求这个二次函数解析式;
(3)P为x轴正半轴上的一点,过点P作与圆A相离并且与x轴垂直的直线,交上述二次函数图像于点F,当⊿CPF中一个内角的正切之为![]() 时,求点P的坐标.
时,求点P的坐标.
答案:
解析:
解析:
|
解:(1)∵点A的坐标为 连结AC,在Rt△AOC中,∠AOC=90°,OA=3,AC=5,∴OC=4. (1分) ∴点C的坐标为 同理可得点B坐标为 (2)设所求二次函数的解析式为 由于该二次函数的图像经过B、C、D三点,则 (3)设点P坐标为 且点F的坐标为 ∵∠CPF=90°,∴当△CPF中一个内角的正切值为 ①若 ②当 所以所求点P的坐标为(12,0). (1分) |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
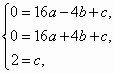 (3分)
(3分)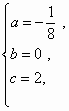
 ,解得
,解得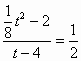 解得
解得 7、如下图,在平面直角坐标系中,A点坐标为(-4,3),将线段OA绕原点O顺时针旋转90°得到OA′,则点A′的坐标是( )
7、如下图,在平面直角坐标系中,A点坐标为(-4,3),将线段OA绕原点O顺时针旋转90°得到OA′,则点A′的坐标是( )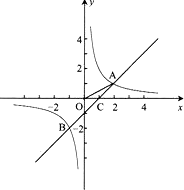
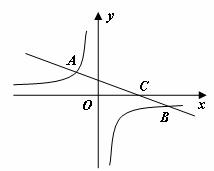
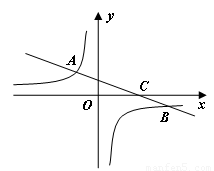
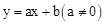 的图像与反比例函数
的图像与反比例函数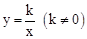 的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),
的图像交于二、四象限的A、B两点,与x轴交于C点。已知A(-2,m),B(n,-2),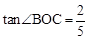 ,则此一次函数的解析式为 .
,则此一次函数的解析式为 .