题目内容
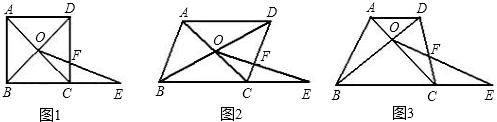
 数学课上,张老师出示了问题:如图:△ABC是等腰直角三角形,∠ACB=90°,AB⊥BF,点P为BC上任意一点,且AP⊥PF,请问:AP与PF相等吗?请说明理由.
数学课上,张老师出示了问题:如图:△ABC是等腰直角三角形,∠ACB=90°,AB⊥BF,点P为BC上任意一点,且AP⊥PF,请问:AP与PF相等吗?请说明理由.如果把“点P是边BC上任意一点”改为“点P是边CB上(除B,C外)延长线上的任意一点”,其它条件不变,那么结论还成立吗?如果正确,请画出图形,写出证明过程.
分析:(1)作FO⊥CB延长线于O点.则∠FBO=45度,BO=FO.由AP⊥PF,很容易知道∠CAP=∠OPF(同角的余角相等),从而△ACP相似于△POF,故可知
=
,其中PO=PB+BO=PB+FO,AC=BC=PB+PC,代入可知FO=CP;从而AC=PO.进一步知道△ACP全等于△POF,AP=PF.(2)同样相等,证明方法同上,先证明△ACP相似于△POF,再证明△ACP全等于△POF即可.
| AC |
| CP |
| PO |
| FO |
解答:解:(1)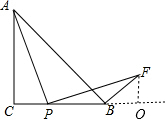
如图作FO⊥CB延长线于O点.
∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠ABC=45°,
又∵AB⊥BF,
∴∠FBO=45°,
∴BO=FO,
又∵AP⊥PF,
∴∠CAP=∠OPF(同角的余角相等),
∴△ACP∽△POF,
∴
=
,
∵PO=PB+BO=PB+FO,AC=BC=PB+PC,
∴FO=CP
∴AC=PO.
在△ACP和△POF中,
,
∴△ACP≌△POF(SAS),
∴AP=PF.
(2)如果“点P是边BC上任意一点”改为“点P是边CB上(除B,C外)延长线上的任意一点”,如图
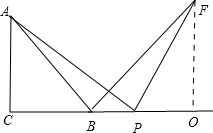
同(1)题可证△ACP∽△POF,
∴
=
,
∵PO=BO-BP=FO-BP,AC=BC=CP-BP,
∴FO=CP
∴AC=PO.
在△ACP和△POF中
∴△ACP≌△POF(SAS),
∴AP=PF.

如图作FO⊥CB延长线于O点.
∵△ABC是等腰直角三角形,∠ACB=90°,
∴∠ABC=45°,
又∵AB⊥BF,
∴∠FBO=45°,
∴BO=FO,
又∵AP⊥PF,
∴∠CAP=∠OPF(同角的余角相等),
∴△ACP∽△POF,
∴
| AC |
| CP |
| PO |
| FO |
∵PO=PB+BO=PB+FO,AC=BC=PB+PC,
∴FO=CP
∴AC=PO.
在△ACP和△POF中,
|
∴△ACP≌△POF(SAS),
∴AP=PF.
(2)如果“点P是边BC上任意一点”改为“点P是边CB上(除B,C外)延长线上的任意一点”,如图

同(1)题可证△ACP∽△POF,
∴
| AC |
| CP |
| PO |
| FO |
∵PO=BO-BP=FO-BP,AC=BC=CP-BP,
∴FO=CP
∴AC=PO.
在△ACP和△POF中
|
∴△ACP≌△POF(SAS),
∴AP=PF.
点评:本题考查了等腰直角三角形的性质,以及全等三角形的判定与性质,正确证明三角形全等的关键是作辅助线.

练习册系列答案
相关题目