题目内容
【题目】如图1,∠AOB=120°,射线OP以1°/秒的速度从OA出发,射线OQ以2°/秒的速度从OB出发,两条射线同时开始逆时针转动t秒.
(1)当t=10秒时,求∠POQ的度数.
(2)如图2,在射线OQ、OP转动过程中,射线OE始终在∠BOQ内部,且OF平分∠AOP,若∠EOF=120°,求![]() 的值.
的值.

【答案】(1)110°;(2)3.
【解析】
(1)根据旋转速度和时间分别求出∠AOP和∠BOQ的度数,再由∠AOB=120°即可求出∠POQ的度数;
(2)根据旋转速度和时间分别求出∠EOQ和∠BOE的度数,即可求出![]() 的值.
的值.
解:(1)当t=10秒时,∠AOP=1°×10=10°,∠BOQ=2°×10=20°,
∵∠AOB=120°,
∴∠POQ=∠AOB﹣∠BOQ+∠AOP=120°﹣20°+10°=110°;
(2)由题意,得∠AOP=t°,∠BOQ=2t°,
∵∠AOB=120°,
∴∠POQ=∠AOB﹣∠BOQ+∠AOP=120°﹣2t°+t°=120°﹣t°,
∵OF平分∠AOP,
∴∠AOF=∠POF=![]() ∠AOP=
∠AOP=![]() t°,
t°,
∵∠AOB=120°,∠EOF=120°,
∴∠BOE=∠AOF=![]() t°,
t°,
∴∠EOQ=∠BOQ﹣∠BOE=2t°﹣![]() t°=
t°=![]() t°,
t°,
∴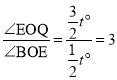

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了了解某校学生的课外阅读情况,随机抽查了![]() 名学生周阅读用时数,结果如下表:
名学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 3 | 4 | 2 | 1 |
则关于这![]() 名学生周阅读所用时间,下列说法正确的是( )
名学生周阅读所用时间,下列说法正确的是( )
A. 中位数是![]() B. 众数是
B. 众数是![]() C. 平均数是
C. 平均数是![]() D. 方差是
D. 方差是![]()







