题目内容
【题目】计算与解方程
(1)|﹣3|+( ![]() ﹣1)0﹣
﹣1)0﹣ ![]() +(
+( ![]() )﹣1;
)﹣1;
(2)解方程组 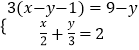 ;
;
(3)求x的值:25(x+2)2﹣36=0.
【答案】
(1)解:原式=3+1﹣4+3
=3
(2)解:原方程可化为 ![]()
①+②得6x=24,
解得x=,4
把x=4代入①得y=0,
所以,原方程组的解为 ![]()
(3)解:方程整理得:(x+2)2= ![]() ,
,
开方得:x+2=± ![]() ,
,
解得:x1=﹣ ![]() ,x2=﹣
,x2=﹣ ![]()
【解析】(1)原式利用立方根的绝对值的性质,零指数幂、负指数幂以及平方根定义化简,然后即可计算出结果.(2)原方程组变形后,直接利用加减消元法从而求出x的值,然后把x的值代入一方程求y的值;(3)方程整理后,利用平方根定义开方即可求出解.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数),以及对整数指数幂的运算性质的理解,了解aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目