题目内容
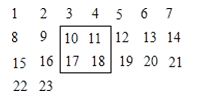
【题目】把2100个连续的正整数1、2、3、……、2100,按如图方式排列成一个数表,如图用一个正方形框在表中任意框住4个数,设左上角的数为x.
(1) 另外三个数用含x的式子表示出来,从小到大排列是___________
(2) 被框住4个数的和为416时,x值为多少?
(3) 能否框住四个数和为324?若能,求出x值;若不能,说明理由
(4) 从左到右,第1至第7列各数之和分别为a1、a2、a3、a4、a5、a6、a7,请直接写出7个数中最大的数与最小的数之差.
【答案】(1)x+1,x+7,x+8;(2)x=100;(3)不能;(4)1800.
【解析】试题分析:(1)根据数表的排列,可用含x的代数式表示出其它三个数;
(2)根据四个数之和为416,可得出关于x的一元一次方程,解之即可得出x的值,再由x不在第7列即可得出结论;
(3)根据四个数之和为324,可得出关于x的一元一次方程,解之即可得出x的值,再由x在第7列即可得出不存在用正方形框出的四个数的和为324;
(4)根据数表的排布,可得出总共300行其每行最右边的数比最左边的数大6,用其×300即可得出结论.
试题解析:解:(1)观察数表可知:另外三个数分别为x+1、x+7、x+8.
故答案为:x+1、x+7、x+8.
(2)设正方形框出的四个数中最小的数为x,根据题意得:x+(x+1)+(x+7)+(x+8)=416,解得:x=100.
∵100=14×7+2,∴100为第2列的数,符合题意.
答:被框住4个数的和为416时,x值为100.
(3)设正方形框出的四个数中最小的数为x,
根据题意得:x+(x+1)+(x+7)+(x+8)=324,解得:x=77,∴77=11×7,∴77为第7列的数,不符合题意,∴不存在用正方形框出的四个数的和为324.
(4)本数表共2100个数,每行7个数,共排300行,即有7列,每列共300个数,∵每一行最右边的数比最左边的数大6,∴a7﹣a1=6×(2100÷7)=1800.
答:7个数中最大的数与最小的数之差为1800.

 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案