题目内容
下列条件能确定△ABC是直角三角形的条件有( )。
(1) ∠A+∠B=∠C; (2) ∠A:∠B:∠C=1:2:3;
(3) ∠A=90°-∠B;
(4) ∠A=∠B=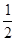 ∠C;
∠C;
A.1个 B.2个 C.3个 D.4个
【答案】
D
【解析】
试题分析:根据三角形的内角和为180°依次分析各小题即可。
(1) ∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴∠C=90°,是直角三角形;
(2) ∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,∴∠C=90°,是直角三角形;
(3) ∵∠A=90°-∠B,∴∠A+∠B=90°,∴∠C=90°,是直角三角形;
(4) ∵∠A=∠B= ∠C,∠A+∠B+∠C=180°,∴∠C=90°,是直角三角形;
∠C,∠A+∠B+∠C=180°,∴∠C=90°,是直角三角形;
故选D.
考点:本题考查的是直角三角形的判定,三角形的内角和定理
点评:解答本题的关键是熟练掌握三角形的内角和为180°,有一个角是90°的三角形是直角三角形.

练习册系列答案
相关题目
在△ABC中,点D、E分别AB、AC上,在下列条件中,不能确定DE∥BC的是( )
| A、AD=2、AB=5、AE=1、CE=1.5 | B、AD=4、AB=6、DE=2、BC=3 | C、AB=3DB、AC=3CE | D、AD:AB=1:3,AE:EC=1:2 |