题目内容
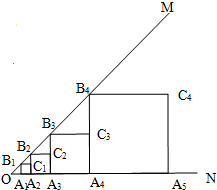 (2013•高要市二模)已知:如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是( )
(2013•高要市二模)已知:如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第6个正方形的面积S6是( )分析:判断出△OA1B1是等腰直角三角形,求出第一个正方形A1B1C1A2的边长为1,再求出△B1C1B2是等腰直角三角形,再求出第2个正方形A2B2C2A3的边长为2,然后依次求出第3个正方形的边长,第4个正方形的边长第5个正方形的边长,第6个正方形的边长,再根据正方形的面积公式列式计算即可得解.
解答:解:∵∠MON=45°,
∴△OA1B1是等腰直角三角形,
∵OA1=1,
∴正方形A1B1C1A2的边长为1,
∵B1C1∥OA2,
∴∠B2B1C1=∠MON=45°,
∴△B1C1B2是等腰直角三角形,
∴正方形A2B2C2A3的边长为:1+1=2,
同理,第3个正方形A3B3C3A4的边长为:2+2=4,
第4个正方形A4B4C4A5的边长为:4+4=8,
第5个正方形A5B5C5A6的边长为:8+8=16,
第6个正方形A6B6C6A7的边长为:16+16=32,
所以,第6个正方形的面积S6是:322=1024.
故选C.
∴△OA1B1是等腰直角三角形,
∵OA1=1,
∴正方形A1B1C1A2的边长为1,
∵B1C1∥OA2,
∴∠B2B1C1=∠MON=45°,
∴△B1C1B2是等腰直角三角形,
∴正方形A2B2C2A3的边长为:1+1=2,
同理,第3个正方形A3B3C3A4的边长为:2+2=4,
第4个正方形A4B4C4A5的边长为:4+4=8,
第5个正方形A5B5C5A6的边长为:8+8=16,
第6个正方形A6B6C6A7的边长为:16+16=32,
所以,第6个正方形的面积S6是:322=1024.
故选C.
点评:本题考查了正方形的性质,等腰直角三角形的判定与性质,得出后一个正方形的边长等于前一个正方形的边长的2倍是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
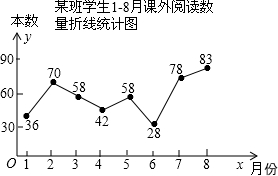 (2013•高要市二模)九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,阅读数量变化率最大的两个月是( )
(2013•高要市二模)九(1)班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,阅读数量变化率最大的两个月是( )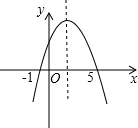 (2013•高要市二模)二次函数y=ax2+bx+c的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x=
(2013•高要市二模)二次函数y=ax2+bx+c的部分图象如图所示,由图象可知该二次函数的图象的对称轴是直线x=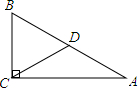 (2013•高要市二模)如图,在△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连结CD.若AC=
(2013•高要市二模)如图,在△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连结CD.若AC=