题目内容
某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为60°,已知在钟摆的摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b-a等于( )A.

B.
 -
-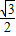
C.
 +
+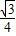
D.
 -
-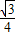
【答案】分析:如图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,所以AD=b,CE=a,CF=b-a,∠AOB=60°求出∠AOC=30°,作AF⊥OC与F,则在△AOC中,可以求出OF,而CF=b-a=OC-OF,由此可以求出b-a的值.
解答: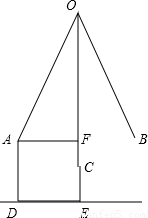 解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,
解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,
所以AD=b,CE=a,CF=b-a,∠AOB=60°,
∴∠AOC=30°.
作AF⊥OC与F,
则在△AOC中,OF=OAcos30°=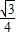 ,
,
∴CF=b-a=OC-OF= -
-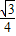 ,
,
∵摆长为0.5米,∴OA=0.5米,
∴OF= ,
,
∴b-a=0.5- ,
,
∴b-a=( -
-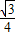 )米.
)米.
故选D.
点评:此题考查直角三角形的性质,解此题的关键是认真分析图形,把实际问题抽象到解直角三角形中来.
解答:
 解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,
解:如上图所示,OA、OB为最大摆幅,OC为摆锤离地最低即和地面垂直时,所以AD=b,CE=a,CF=b-a,∠AOB=60°,
∴∠AOC=30°.
作AF⊥OC与F,
则在△AOC中,OF=OAcos30°=
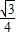 ,
,∴CF=b-a=OC-OF=
 -
-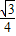 ,
,∵摆长为0.5米,∴OA=0.5米,
∴OF=
 ,
,∴b-a=0.5-
 ,
,∴b-a=(
 -
-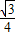 )米.
)米.故选D.
点评:此题考查直角三角形的性质,解此题的关键是认真分析图形,把实际问题抽象到解直角三角形中来.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
某落地钟钟摆的摆长为0.5米,来回摆动的最大夹角为60°,已知在钟摆的摆动过程中,摆锤离地面的最低高度为a米,最大高度为b米,则b-a等于( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|


