题目内容
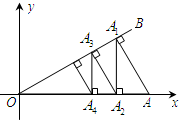 (2013•平遥县模拟)如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作AA1⊥OB,垂足为A1;过A1作A1A2⊥x轴,垂足为A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为A4…;这样一直作下去,则A2013的纵坐标为
(2013•平遥县模拟)如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0).过A作AA1⊥OB,垂足为A1;过A1作A1A2⊥x轴,垂足为A2;再过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为A4…;这样一直作下去,则A2013的纵坐标为(
)2013
| ||
| 2 |
(
)2013
.
| ||
| 2 |
分析:根据锐角三角函数关系得出A1A2,A2A3…的长,进而得出各点的纵坐标关系,进而得出规律求出答案.
解答:解:过A作AA1⊥OB,垂足为A1;过A1作A1A2⊥x轴,过点A2作A2A3⊥OB,垂足为点A3;再过点A3作A3A4⊥x轴,垂足为A4…
∵∠AOB=30°,点A坐标为(2,0),
∴A1A=
AO=1,
∴A1A2=A1A×cos30°=
,
∴A2A3=A1A2×cos30°=
×
,
…
则A2013的纵坐标A2013A2014=(
)2013.
故答案为:(
)2013.
∵∠AOB=30°,点A坐标为(2,0),
∴A1A=
| 1 |
| 2 |
∴A1A2=A1A×cos30°=
| ||
| 2 |
∴A2A3=A1A2×cos30°=
| ||
| 2 |
| ||
| 2 |
…
则A2013的纵坐标A2013A2014=(
| ||
| 2 |
故答案为:(
| ||
| 2 |
点评:此题主要考查了点的坐标规律,根据已知得出点A纵坐标变化规律是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
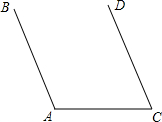 (2013•平遥县模拟)如图,AB∥CD,∠BAC=120°,则∠C的度数是( )
(2013•平遥县模拟)如图,AB∥CD,∠BAC=120°,则∠C的度数是( )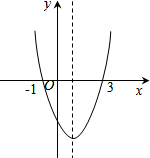 (2013•平遥县模拟)如图是二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②a+b+c>0;③4a-2x+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )
(2013•平遥县模拟)如图是二次函数y=ax2+bx+c的图象,在下列说法中:①abc>0;②a+b+c>0;③4a-2x+c>0;④当x>1时,y随着x的增大而增大.正确的说法个数是( )