题目内容
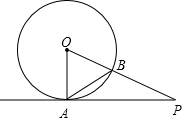如图，PA为⊙O的切线，A为切点，PO交⊙O于点B，OA=3，OP=6，那么∠BAP的度数是（ ）| A、30° | B、45° | C、60° | D、35° |
分析：根据切线的性质可知，OA⊥PA；Rt△OAP中，已知OA=3，OP=6，易求得∠OPA的正弦值，即可得出∠OPA的度数，再根据等腰三角形及直角三角形的性质解答即可．
解答：解：∵PA为⊙O的切线，A为切点，
∴OA⊥PA，
∴∠OAP=90°；
在Rt△OAP中，
∵sin∠OPA=
=
=
，
∴∠OPA=30°，
∴∠AOP=90°-∠OPA=90°-30°=60°；
在△OAB中，
∵∠AOP=60°，OA=OB，
∴∠OAB=60°，
∴∠BAP=∠OAP-∠OAB=90°-60°=30°．
故选A．
∴OA⊥PA，
∴∠OAP=90°；
在Rt△OAP中，
∵sin∠OPA=
| OA |
| OP |
| 3 |
| 6 |
| 1 |
| 2 |
∴∠OPA=30°，
∴∠AOP=90°-∠OPA=90°-30°=60°；
在△OAB中，
∵∠AOP=60°，OA=OB，
∴∠OAB=60°，
∴∠BAP=∠OAP-∠OAB=90°-60°=30°．
故选A．
点评：本题考查的是切线的性质、特殊角的三角函数及直角三角形的性质．
练习册系列答案
阅读快车系列答案
相关题目
7、如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=60°，则∠P的度数为（ ）
4、如图，PA、PB分别切⊙O于A、B两点，如果∠P=60°，PA=2，那么AB的长为（ ）
6、如图，PA、PB分别切⊙O于点A、B，M是劣弧AB上的一个动点（点A、B除外），过M作⊙O的切线分别交PA、PB于点C、D．设CM的长为x，△PCD的周长为y，在下列图象中，大致表示y与x之间的函数关系的是（ ）
（2012•莆田质检）如图，PA、PB分别切⊙O于A、B两点，点C在优弧
如图，PA，PB分别切⊙O于点A和点B，C是