题目内容
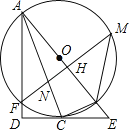
【题目】如图，⊙O是△ABC的外接圆，FH是⊙O的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．（1）证明：AF平分∠BAC；（2）证明：BF=FD；（3）若EF=4，DE=3，求AD的长．
【答案】
【1】 见解析
【2】 见解析
【3】 
【解析】
证明：（1）连接OF
∴FH切·O于点F
∴OF⊥FH ………………………… 1分
∵BC | | FH
∴OF⊥BC ………………………… 2分
∴BF="CF" ………………………… 3分
∴∠BAF=∠CAF
即AF平分∠BAC…………………4分
（2） ∵∠CAF=∠CBF
又∠CAF=∠BAF
∴∠CBF=∠BAF ………………………… 6分
∵BD平分∠ABC
∴∠ABD=∠CBD
∴∠BAF+∠ABD=∠CBF+∠CBD
即∠FBD=∠FDB………………………… 7分
∴BF="DF" ………………………… 8分
（3） ∵∠BFE=∠AFB ∠FBE=∠FAB
∴ΔBEF∽ΔABF………………………… 9分
∴
即BF2=EF·AF …………………… 10分
∵EF=4 DE=3 ∴BF="DF" =4+3=7
AF=AD+7
即4（AD+7）=49 解得AD=
练习册系列答案
相关题目
