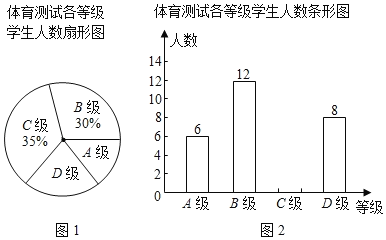
ЬтФПФкШн
ЁОЬтФПЁПдкRtЁїABCжа,ЁЯACB= 90Ёу,AC= 6cm, AB= 12cm,ЕуP ДгAГіЗЂбиACЯђCЕувд1cm/sЕФЫйЖШдШЫйвЦЖЏ;ЕуQДгCГіЗЂбиCBЯђBЕувд![]() cm/sЕФЫйЖШдШЫйвЦЖЏЃЌЕуPЁЂQЗжБ№ДгЦ№ЕуЭЌЪБГіЗЂЃЌвЦЖЏЕНФГвЛЮЛжУЪБЫљашЪБМфЮЊtУы;Еу0ЮЊABЕФжаЕуЁЃ
cm/sЕФЫйЖШдШЫйвЦЖЏЃЌЕуPЁЂQЗжБ№ДгЦ№ЕуЭЌЪБГіЗЂЃЌвЦЖЏЕНФГвЛЮЛжУЪБЫљашЪБМфЮЊtУы;Еу0ЮЊABЕФжаЕуЁЃ
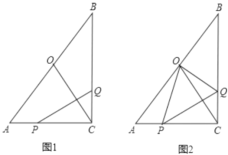
(1)ЕБt=2ЪБЃЌЧѓЯпЖЮPQЕФГЄЖШ;
(2) СЌНгOC,ЕБPQЁЭ0CЪБЃЌЧѓГіtЕФжЕ;
(3)СЌНсPOЃЌPQ,ЪЧЗёДцдкtЕФжЕЃЌЪЙЁїOPQГЩЮЊвдPQЮЊаББпЕФжБНЧШ§НЧаЮ?ШєДцдкЃЌЧѓГіtЕФжЕ;ШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉДцдкЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉгУдЫЖЏЪБМфЪЧ2УыЃЌЧѓГіPCЃЌCQдйгУЙДЙЩЖЈРэЧѓНтМДПЩЃЛ
ЃЈ2ЃЉгЩжБНЧШ§НЧаЮЕФаджЪЃЌХаЖЯГіЁЯACO=60ЁуЃЌНсКЯPQЁЭOCЕУГіЁЯCPQ=30ЁуЃЌРћгУШ§НЧКЏЪ§ЧѓНтМДПЩЃЛ
ЃЈ3ЃЉРћгУжБНЧШ§НЧаЮЕФаджЪКЭжаЮЛЯпЃЌЕУГіЁЯPON=ЁЯMOQЃЌдйгУЕШНЧЕФе§ЧажЕЯрЕШНЈСЂЗНГЬЃЌЗжСНжжЧщПіЬжТлМЦЫуМДПЩЃЎ
НтЃКЁпЕуPДгAГіЗЂбиACЯђCЕувд1cm/sЕФЫйЖШдШЫйвЦЖЏЃЌ
ЁрAP=tЃЌ
ЁрCP=6-tЃЌ
ЁпЕуQДгCГіЗЂбиCBЯђBЕувд![]() cm/sЕФЫйЖШдШЫйвЦЖЏЃЌ
cm/sЕФЫйЖШдШЫйвЦЖЏЃЌ
Ёр![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЕБt=2ЪБЃЌPC=4ЃЌCQ=![]() ЃЌ
ЃЌ
ЁпЁЯACB=90ЁуЃЌ
ИљОнЙДЙЩЖЈРэЕУЃЌ![]() ЃЌ
ЃЌ
ЃЈ2ЃЉдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=6cmЃЌAB=12cmЃЌ
ЁрЁЯB=30ЁуЃЌЁЯA=60ЁуЃЌBC=![]()
![]() ЃЌ
ЃЌ
ЁпЕуOЮЊABжаЕуЃЌ
ЁрOA=OCЃЌ
ЁрЁЯACO=60ЁуЃЌ
ЩшOCКЭPQЕФНЛЕуЮЊDЃЌ
ЁрPQЁЭOCЃЌ
ЁрЁЯPDC=90ЁуЃЌ
ЁрЁЯCPQ=30ЁуЃЌ
дкRtЁїPCQжаЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЃЈ3ЃЉДцдкЃЌШчЭМ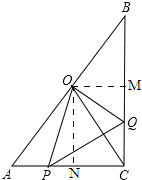
Й§ЕуOзїONЁЭACЃЌOMЁЭBCЃЌ
ЁпЕуOЪЧABжаЕуЃЌ
Ёр![]()
![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁпЁїOPQГЩЮЊвдPQЮЊаББпЕФжБНЧШ§НЧаЮЃЌ
ЁрЁЯPON=ЁЯMOQЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
Ђй ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
Ђк ЕБ![]() ЪБЃЌ
ЪБЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЈЩсЃЉЃЌДЫжжЧщПіВЛДцдкЃЛ
ЃЈЩсЃЉЃЌДЫжжЧщПіВЛДцдкЃЛ
МДЃКДцдкЃЌ![]() ЪБЃЌЁїOPQГЩЮЊвдPQЮЊаББпЕФжБНЧШ§НЧаЮЃЎ
ЪБЃЌЁїOPQГЩЮЊвдPQЮЊаББпЕФжБНЧШ§НЧаЮЃЎ