题目内容
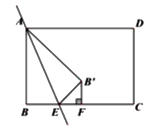
【题目】如图，矩形ABCD中，AB=5，BC=7，E为BC上的动点，将矩形沿直线AE翻折，使点B的对应点B＇落在∠ADC的平分线上，过点B＇作B＇F⊥BC于点F，求△B＇EF的周长______.
【答案】4或6．
【解析】
连接B′D，过点B′作B′M⊥AD于M，根据点B′落在∠ADC的角平分线上，可知三角形△DMB′是等腰直角三角形，设DM=B′M=x，在直角△AMB′中，由勾股定理列出方程求出x的值，然后分情况求周长即可.
解：连接B′D，过点B′作B′M⊥AD于M．
∵点B的对应点B′落在∠ADC的角平分线上，
∴设DM=B′M=x，则AM=7-x，
又由折叠的性质知AB=AB′=5，
∴在直角△AMB′中，由勾股定理得：
，即（7-x）
=25-x，
解得x=3或x=4，
当x=3时，AM=4，B′F=2，△B′EF的周长=B′E+EF+ B′F=BE+EF+ B′F=4+2=6，
当x=4时，同理可得△B′EF的周长=4，
∴△B′EF的周长为4或6．
故答案为：4或6．
练习册系列答案
小学期末标准试卷系列答案
相关题目
