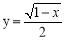题目内容
若一列不全为零的数除了第一个数和最后一个数外,每个数都等于前后与它相邻的两数之和,则称这列数具有“波动性质”.已知一列数共有18个,且具有“波动性质”,则这18个数的和为( )
A.-64 B.0 C.18 D.64
B.
【解析】
试题分析:由题意得:
an+2=an+1+an+3,
an+3=an+2+an+4,
两式相加,得:an+an+2+an+4=0;
同理可得:
an+1+an+3+an+5=0,
以上两式相加,可知: 该数列连续六个数相加等于零,18是6的倍数,所以结果为零.
故选B.
考点:1.新定义;2.探索规律题(数字的变化类).

练习册系列答案
相关题目