题目内容
已知二次函数y=kx2+(2k-1)x-1的图象与x轴交点的横坐标为x1,x2(x1<x2),那么下列结论:①方程kx2+(2k-1)x-1=0的两根为x1,x2;②当x>x2时,y>0;③x1<-1,x2>-1;④x2-x1=
| ||
| k |
分析:①根据一元二次方程和二次函数之间的联系即可判断;②由于k值不确定,所以抛物线的开口方向不确定,所以该题的结论不一定成立;③可以判断(x1+1)(x2+1)的符号;④根据一元二次方程的根与系数的关系以及完全平方公式进行分析.
解答:解:①二次函数y=kx2+(2k-1)x-1的图象与x轴交点的横坐标,即为令y=0方程的两个根,故该结论正确;
②由于k值不确定,所以抛物线的开口方向可能向下,故该结论不一定成立;
③根据一元二次方程根与系数的关系,得x1+x2=
,x1x2=-
,
则(x1+1)(x2+1)=x1x2+x1+x2+1=-
+
+1=-1<0,所以x1<-1,x2>-1,故该结论成立;
④x2-x1=
=
,由于k的符号不确定,故该选项错误.
故答案为①③.
②由于k值不确定,所以抛物线的开口方向可能向下,故该结论不一定成立;
③根据一元二次方程根与系数的关系,得x1+x2=
| 1-2k |
| k |
| 1 |
| k |
则(x1+1)(x2+1)=x1x2+x1+x2+1=-
| 1 |
| k |
| 1-2k |
| k |
④x2-x1=
| (x1+x2)2-4x1x2 |
|
故答案为①③.
点评:此题考查了一元二次方程和二次函数之间的联系,能够熟练运用一元二次方程根与系数的关系以及完全平方公式的变形.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
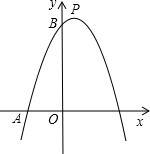 点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过点A、点B.
点B,顶点为P,且OB=3OA,一次函数y=kx+b的图象经过点A、点B. 已知二次函数y=ax2+bx+3图象的对称轴为直线x=1.
已知二次函数y=ax2+bx+3图象的对称轴为直线x=1. 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.