题目内容
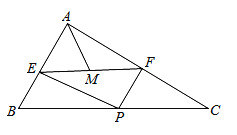
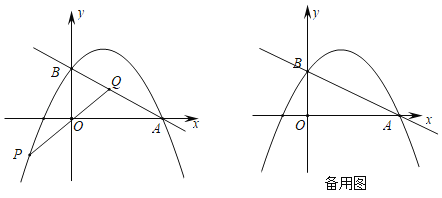
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)当t=4时,求点E的坐标;
(2)在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)点E的坐标是(8,0);(2)存在,P的坐标为:(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).
【解析】
(1)过点E作CB的垂线,垂足为H,首先证明△PBC∽△BEH,然后由相似三角形的性质求出BH=6,得出OE=8即可求出点E的坐标;
(2)本题需先证出△BCP∽△BAE,求出AE=![]() t,再分四种情况讨论:①点P在点O上方时,△POE∽△EAB;②点P在点O上方时,△POE∽△BAE;③当点P在点O下方时,△OPE∽△ABE;④当点P在点O下方时,△OEP∽△ABE;分别求解即可.
t,再分四种情况讨论:①点P在点O上方时,△POE∽△EAB;②点P在点O上方时,△POE∽△BAE;③当点P在点O下方时,△OPE∽△ABE;④当点P在点O下方时,△OEP∽△ABE;分别求解即可.
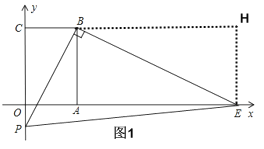
解:(1)当t=4时,PC=4,
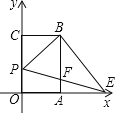
过点E作CB的垂线,垂足为H,如图1所示:
∵A(2,0),C(0,3),
∴OA=2,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=2,
∵∠BPC+∠PBC=90°,∠PBC+∠EBH=90°,
∴∠BPC=∠EBH,
∵∠EHB=∠BCP=90°,
∴△PBC∽△BEH,
∴![]() ,即
,即![]() =
=![]() ,
,
解得:BH=6,
∴AE=BH=6,
∴OE=OA+AE=2+6=8,
∴点E的坐标是(8,0);
(2)存在;
∵∠ABE+∠ABP=90°,∠PBC+∠ABP=90°,
∴∠ABE=∠PBC,
∵∠BAE=∠BCP=90°,
∴△BCP∽△BAE,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() t,
t,
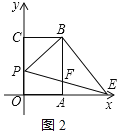
当点P在点O上方时,如图2所示:
①若![]() 时,△POE∽△EAB,
时,△POE∽△EAB,
∵OP=3﹣t,OE=2+![]() t,
t,
∴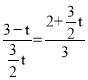 ,
,
解得:t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
∴OP=3﹣![]() =
=![]() ,
,
∴P的坐标为(0,![]() );
);
②若△POE∽△BAE,
∵∠PEO和∠BEA明显不相等,
∴此情况不成立;
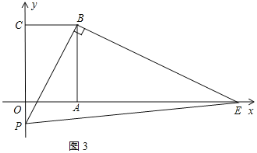
当点P在点O下方时,如图3所示:
③若![]() ,则△OPE∽△ABE,
,则△OPE∽△ABE,
∴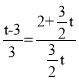 ,
,
解得:t1=3+![]() ,t2=3﹣
,t2=3﹣![]() (舍去),
(舍去),
OP=t﹣3=3+![]() ﹣3=
﹣3=![]() ,
,
∴P的坐标为(0,﹣![]() );
);
④若![]() ,则△OEP∽△ABE,
,则△OEP∽△ABE,
即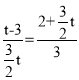 ,整理得:
,整理得:![]() t2=﹣9,
t2=﹣9,
∴这种情况不成立,
综上所述,存在以P、O、E为顶点的三角形与△ABE相似,P的坐标为:(0,![]() )或(0,﹣
)或(0,﹣![]() ).
).

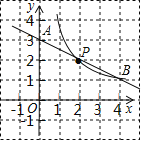
【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).