题目内容
 平面直角坐标系内有两条直线l1、l2,直线l1的解析式为y=-
平面直角坐标系内有两条直线l1、l2,直线l1的解析式为y=-| 2 | 3 |
(1)求直线l2的解析式;
(2)设直线l1与l2相交于点M,问:是否存在这样的直线l:y=x+t,使得如果将坐标纸沿直线l折叠,点M恰好落在x轴上?若存在,求出直线l的解析式;若不存在,请说明理由;
(3)设直线l2与x轴、y轴分别交于点A、B,点P(a,0)在x轴正半轴上运动,点Q(0,b)在y轴负半轴上运动,且PQ⊥AB,若△APQ是等腰三角形,求a,b.
分析:(1)先求出在直线l1上的两个点的坐标,然后折叠再求出相应的两点坐标,最后求出直线l2的解析式;
(2)先求出点M的坐标,然后根据题中已知条件看是否存在直线1;
(3)求出A、B的坐标,然后根据△APQ是等腰三角形,且PQ⊥AB来求出a,b.
(2)先求出点M的坐标,然后根据题中已知条件看是否存在直线1;
(3)求出A、B的坐标,然后根据△APQ是等腰三角形,且PQ⊥AB来求出a,b.
解答: 解:如图所示:
解:如图所示:
(1)∵点(-2,0)与点(0,2)重合,可知折叠痕迹为y=-x;
直线l1经过点(0,1),(1.5,0).
可知对称的点为(-1,0),(0,-1.5).
设直线l2解析式为:y=kx+b;
将点的坐标代入可得:
,
解得:
;
则直线l2的解析式为:y=-1.5x-1.5;
(2)直线l1与l2相交于点M,
则M的坐标为(-3,3);
因为直线1的斜率为k=1,
而点M关于斜率为1的直线的对称点必在直线y=-x上面,
所以点M关于直线l的对称点为O(0,0),
可知点M和点O关于(-1.5,1.5)对称,
将点(-1.5,1.5)代入直线l中可得解析式为:y=x+3;
所以存在直线l:y=x+3,使得如果将坐标纸沿直线l折叠,点M恰好落在x轴上;
(3)根据直线l2解析式可得A(-1,0),B(0,-1.5);
因为PQ⊥AB可知直线PQ的斜率为k=-
=
;
可设b=-2t,则a=3t,t>0;
①AQ=PQ,则PO=AO,
所以a=1,b=-
;
②当AP=AQ,3t+1=
?t=0或t=-
,
不合题意,舍去;
③当AP=PQ,3t+1=
t,
解得t=
或t=
(舍去),a=
,b=-
;
所以
或
.
 解:如图所示:
解:如图所示:(1)∵点(-2,0)与点(0,2)重合,可知折叠痕迹为y=-x;
直线l1经过点(0,1),(1.5,0).
可知对称的点为(-1,0),(0,-1.5).
设直线l2解析式为:y=kx+b;
将点的坐标代入可得:
|
解得:
|
则直线l2的解析式为:y=-1.5x-1.5;
(2)直线l1与l2相交于点M,
则M的坐标为(-3,3);
因为直线1的斜率为k=1,
而点M关于斜率为1的直线的对称点必在直线y=-x上面,
所以点M关于直线l的对称点为O(0,0),
可知点M和点O关于(-1.5,1.5)对称,
将点(-1.5,1.5)代入直线l中可得解析式为:y=x+3;
所以存在直线l:y=x+3,使得如果将坐标纸沿直线l折叠,点M恰好落在x轴上;
(3)根据直线l2解析式可得A(-1,0),B(0,-1.5);
因为PQ⊥AB可知直线PQ的斜率为k=-
| b |
| a |
| 2 |
| 3 |
可设b=-2t,则a=3t,t>0;
①AQ=PQ,则PO=AO,
所以a=1,b=-
| 2 |
| 3 |
②当AP=AQ,3t+1=
| 1+ 4t2 |
| 6 |
| 5 |
不合题意,舍去;
③当AP=PQ,3t+1=
| 13 |
解得t=
6+2
| ||
| 8 |
6-2
| ||
| 8 |
9+3
| ||
| 4 |
3+
| ||
| 2 |
所以
|
|
点评:本题主要考查对于二元一次方程组的应用以及对于对称图形的掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围. x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.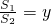 ,求y与x之间的函数关系式
,求y与x之间的函数关系式 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围. x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合. )为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)
)为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)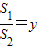 ,求y与x之间的函数关系式,并写出自变量x的取值范围.
,求y与x之间的函数关系式,并写出自变量x的取值范围.