题目内容
如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数 的图象的一个交点为A(1,m) .过点B作AB的垂线BD,与反比例函数
的图象的一个交点为A(1,m) .过点B作AB的垂线BD,与反比例函数 (x>0)的图象交于点D(n,-2).
(x>0)的图象交于点D(n,-2).
(1)求k1和k2的值;
(2)若直线AB、BD分别交x轴于点C、E,试问在y轴上是否存在一点F,使得△BDF∽△ACE.若存在,求出点F的坐标;若不存在,请说明理由.
(1)k1=4、k2=-16。
(2)存在符合条件的F坐标为(0,-8)
解析分析:(1)将A坐标代入一次函数解析式中求出m的值,确定出A的坐标,将A坐标代入反比例函数
中即可求出k1的值;
过A作AM垂直于y轴,过D作DN垂直于y轴,可得出一对直角相等,再由AC垂直于BD,利用同角的余角相等得到一对角相等,利用两对对应角相等的两三角形相似得到△ABM与△BDN相似,由相似得比例,求出DN的长,确定出D的坐标,代入反比例函数 中即可求出k2的值;
中即可求出k2的值;
(2)在y轴上存在一个点F,使得△BDF∽△ACE,此时F(0,-8),理由为:由y=2x+2求出C坐标,由OB=ON=2,DN=8,可得出OE为△BDN的中位线,求出OE的长,进而利用勾股定理求出AE,CE,AC,BD的长,以及∠EBO=∠ACE=∠EAC,若△BDF∽△ACE,得到比例式,求出BF的长,即可确定出此时F的坐标。
解:(1)将A(1,m)代入一次函数y=2x+2中,得:m=2+2=4,
∴A(1,4)。
将A(1,4)代入反比例解析式 得:k1=4。
得:k1=4。
过A作AM⊥y轴于点M,过D作DN⊥y轴于点N,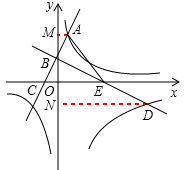
∴∠AMB=∠DNB=90°。∴∠BAM+∠ABM=90°。
∵AC⊥BD,即∠ABD=90°,
∴∠ABM+∠DBN=90°。∴∠BAM=∠DBN。
∴△ABM∽△BDN。∴ ,即
,即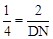 。∴DN=8。
。∴DN=8。
∴D(8,-2)。
将D坐标代入 得:k2=-16。
得:k2=-16。
(2)存在符合条件的F坐标为(0,-8)。理由如下:
由y=2x+2,求出C坐标为(-1,0)。
∵OB=ON=2,DN=8,∴OE=4。
可得AE=5,CE=5,AC=2 ,BD=4
,BD=4 ,∠EBO=∠ACE=∠EAC。
,∠EBO=∠ACE=∠EAC。
若△BDF∽△ACE,则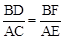 ,即
,即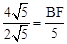 ,解得:BF=10。
,解得:BF=10。
∴F(0,-8)。
∴存在符合条件的F坐标为(0,-8)。

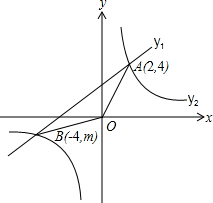 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数