Question

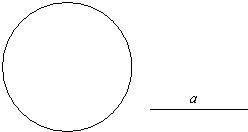18、已知：一个定圆，一条线段a．
求作：这个定圆的内接等腰三角形，使该等腰三角形的底边为a．
（要求保留作图痕迹，不要求写作法．）

Answer 1

分析：根据垂径定理和勾股定理，可以首先确定弦心距，再进一步作弦，即可作出圆的内接等腰三角形．

解答：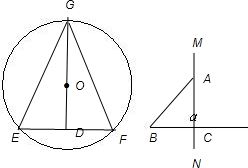

解：（1）根据垂径定理的推论，即可确定圆心和园的半径，即两条弦的垂直平分线的交点即为圆心；
（2）以线段a的一半为直角边、以圆的半径为斜边作一直角三角形ABC；
（3）在圆中，作线段OD=AC，DO的延长线和圆交于点G；
（4）作EF⊥OD，和圆交于点E、F；
（5）连接EG、FG．
则△EFG即为所求作的三角形．

点评：此题综合运用了勾股定理和垂径定理．