题目内容
【题目】有一边是另一边的
倍的三角形叫做智慧三角形，这两边中较长边称为智慧边，这两边的 夹角叫做智慧角．
（1）在 Rt△ABC 中，∠ACB＝90°，若∠A 为智慧角，则∠B 的度数为 ；
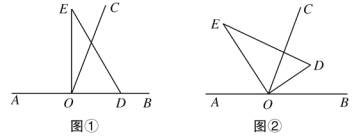
（2）如图①，在△ABC 中，∠A＝45°，∠B＝30°，求证：△ABC 是智慧三角形；
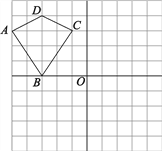
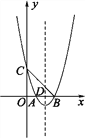
（3）如图②，△ABC 是智慧三角形，BC 为智慧边，∠B 为智慧角，A（3，0），点 B，C 在函数 y＝
（x＞0）的图像上，点 C 在点 B 的上方，且点 B 的纵坐标为
．当△ABC是直角三角形时，求 k 的值．
【答案】（1）45°．（2）见解析；（3）k＝4
或18＋15
．
【解析】试题分析：（1）由智慧角的定义得到AB=
AC，解直角三角形即可得到结论．
（2）过点C作CD⊥AB于点D．在Rt△ACD中，由∠A＝45°，得到AC＝
DC．
在Rt△BCD中，由∠B＝30°，得到BC＝2DC，即可得到结论．
（3）分两种情况讨论：①∠ABC＝90°；②∠BAC＝90°．
试题解析：解：（1）∵∠ACB＝90°，若∠A 为智慧角，∴AB=
AC，∴cosA=
，∴∠A=45°，∴∠B=45°．
（2）如图1，过点C作CD⊥AB于点D．
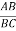
在Rt△ACD中，∠A＝45°，∴AC＝
DC．
在Rt△BCD中，∠B＝30°，∴BC＝2DC，∴
＝
，∴△ABC是智慧三角形．
（3）由题意可知：∠ABC＝90°或∠BAC＝90°．
①当∠ABC＝90°时，如图2，过点B作BE⊥x轴于点E，过点C作CF⊥EB交EB延长线于点F，过点C作CG⊥x轴于点G，则∠AEB＝∠F＝∠ABC＝90°，∴∠BCF＋∠CBF＝∠ABE＋∠CBF＝90°，∴∠BCF＝∠ABE，∴△BCF∽△ABE，∴
＝
＝
＝
．
设AE＝a，则BF＝
a．∵BE＝
，∴CF＝2．
∵OG＝OA＋AE－GE＝3＋a－2＝1＋a，CG＝EF＝
＋
a，∴B（3＋a， 
），C（1＋a， 
＋
a）．∵点B，C在函数y＝
（x＞0）的图像上，∴
(3＋a)＝(1＋a)( 
＋
a)＝k．
解得：a1＝1，a2＝－2（舍去），∴k＝
．
②当∠BAC＝90°时，如图3，过点C作CM⊥x轴于点M，过点B作BN⊥x轴于点N，则∠CMA＝∠CAB＝∠ANB＝90°，∴∠MCA＋∠CAM＝∠BAN＋∠CAM＝90°，∴∠MCA＝∠BAN．由（1）知∠B＝45°，∴△ABC是等腰直角三角形，∴AC＝AB．
由①知△MAC∽△NBA，∴△MAC≌△NBA（AAS），∴AM＝BN＝
．
设CM＝AN＝b，则ON＝3＋b，∴B（3＋b， 
），C（3－
，b）．
∵点B，C在函数y＝
（x＞0）的图像上，∴
(3＋b)＝(3－
)b＝k，
解得：b＝9
＋12，∴k＝18＋15
．
综上所述：k＝4
或18＋15
．
