题目内容
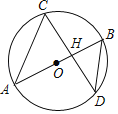
【题目】如图,![]() 分别是正方形
分别是正方形![]() 的边
的边![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() ,如下结论:①
,如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中,正确的结论有( )
.其中,正确的结论有( )
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/22/2490290299265024/2493010512084992/STEM/52fa12adf3724617abc1f4d89e19890c.png]
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由AG=CE知BG=BE,根据勾股定理可得![]() ,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△AGE≌△ECF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.
,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△AGE≌△ECF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.
∵四边形ABCD是正方形,
∴AB=BC=CD,∠B=∠C=∠D=90°
∵AG=CE,
∴BG=BE,
∴![]()
∴![]() ,故①正确;
,故①正确;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△AGE和△ECF中,
∵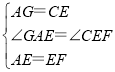
∴△AGE≌△ECF(SAS),∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°-90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
故选:C.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目