题目内容
【题目】如图，在四边形ABCD中，AB=DC，P是对角线AC的中点，M是AD的中点，N是BC的中点．
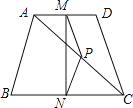
（1）若AB=6，求PM的长；
（2）若∠PMN=20°，求∠MPN的度数．
【答案】（1）3；（2）140°．
【解析】
试题分析：（1）由题意可知PM是△ADC的中位线，进而可求出MP的长；
（2）易证△PMN是等腰三角形，由等腰三角形的性质即可求出∠MPN的度数．
试题解析：（1）∵AB=DC，AB=6，
∴DC=6，
∵点P是AC的中点，点M是AD的中点，
∴PM=
DC=×6=3；
（2）∵点P是AC的中点，点N是BC的中点，
∴PN=BC，
∵AB=DC，
∴PM=PN，
∴∠PNM=∠PMN=20°，
∴∠MPN=180°-∠PMN-∠PNM=140°．
练习册系列答案
相关题目