题目内容
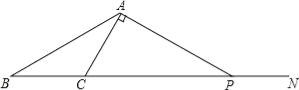
【题目】如图,点N是△ABC的边BC延长线上的一点,∠ACN=2∠BAC,过点A作AC的垂线交CN于点P.
(1)若∠APC=30°,求证:AB=AP;
(2)若AP=8,BP=16,求AC的长;
(3)若点P在BC的延长线上运动,∠APB的平分线交AB于点M.你认为∠AMP的大小是否发生变化?若变化,请说明理由;若不变化,求出∠AMP的大小.
【答案】(1)、证明过程见解析;(2)、6;(3)、45°.
【解析】
试题分析:(1)、由∠P=30°,∠CAP=90°得∠ACP=60°,∠BAC=30°,所以∠ABP=30°,进而可得∠ABP=∠P,即AB=AP;(2)、设AC=x,由勾股定理建立方程得x2+82=(16﹣x)2求出x的值即可求出AC的长;
(3)、∠AMP的大小不发生变化,由∠AMP=∠B+∠APC=![]() ∠ACP+
∠ACP+![]() ∠APC=
∠APC=![]() (∠ACP+∠APC)=
(∠ACP+∠APC)=![]() 90°=45°进而可得结论.
90°=45°进而可得结论.
试题解析:(1)、∵AC⊥AP, ∴∠CAP=90°, ∵∠P=30°, ∴∠ACP=60°, ∴∠BAC=30°,
∴∠ABP=30°, ∴∠ABP=∠P, ∴AB=AP;
(2)、设AC=x,在Rt△ACP中,由勾股定理建立方程得x2+82=(16﹣x)2 解得x=6, 所以AC=6;
(3)、∠AMP的大小不发生变化
理由如下: ∵∠AMP=∠B+![]() ∠APC=
∠APC=![]() ∠ACP+
∠ACP+![]() ∠APC=
∠APC=![]() (∠ACP+∠APC)=
(∠ACP+∠APC)=![]() 90°=45°,
90°=45°,
∴是一个的值,即不发生变化.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目