题目内容
已知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是
- A.16

- B.16
- C.8

- D.8
C
分析:首先由四边形ABCD是菱形,求得AC⊥BD,OA= AC,∠BAC=
AC,∠BAC= ∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.
∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.
解答: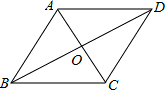 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC= AC=
AC= ×4=2,∠BAC=
×4=2,∠BAC= ∠BAD=
∠BAD= ×120°=60°,
×120°=60°,
∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB=2 ,
,
∴BD=2OB=4 ,
,
∴该菱形的面积是: AC•BD=
AC•BD= ×4×4
×4×4 =8
=8 .
.
故选C.
点评:此题考查了菱形的性质,直角三角形的性质.解题的关键是注意数形结合与方程思想的应用,注意菱形的面积等于其对角线积的一半.
分析:首先由四边形ABCD是菱形,求得AC⊥BD,OA=
 AC,∠BAC=
AC,∠BAC= ∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.
∠BAD,然后在直角三角形AOB中,利用30°角所对的直角边等于斜边的一半与勾股定理即可求得OB的长,然后由菱形的面积等于其对角线积的一半,即可求得该菱形的面积.解答:
 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,∴AC⊥BD,OA=OC=
 AC=
AC= ×4=2,∠BAC=
×4=2,∠BAC= ∠BAD=
∠BAD= ×120°=60°,
×120°=60°,∴AC=4,∠AOB=90°,
∴∠ABO=30°,
∴AB=2OA=4,OB=2
 ,
,∴BD=2OB=4
 ,
,∴该菱形的面积是:
 AC•BD=
AC•BD= ×4×4
×4×4 =8
=8 .
.故选C.
点评:此题考查了菱形的性质,直角三角形的性质.解题的关键是注意数形结合与方程思想的应用,注意菱形的面积等于其对角线积的一半.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
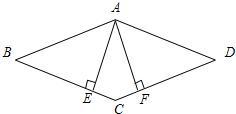 18、如图,已知菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F.
18、如图,已知菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F.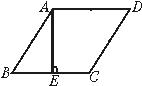 4、如图,已知菱形ABCD中,AE⊥BC于E,若S菱形ABCD=48,且AE=6,则菱形的边长为( )
4、如图,已知菱形ABCD中,AE⊥BC于E,若S菱形ABCD=48,且AE=6,则菱形的边长为( )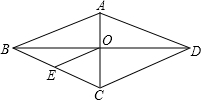 (2013•丰南区一模)如图,已知菱形ABCD中,对角线AC与BD相交于点O,OE∥DC,交BC于点E,AD=6cm,则OE的长为( )
(2013•丰南区一模)如图,已知菱形ABCD中,对角线AC与BD相交于点O,OE∥DC,交BC于点E,AD=6cm,则OE的长为( )