Question

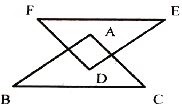
【题目】如图，观察每个正多边形中的变化情况，解答下列问题：

（1）将下面的表格补充完整：

正多边形的边数	3	4	5	6	…	15
的度数					…

（2）根据规律，是否存在一个正边形，使其中？若存在，直接写出的值；若不存在，请说明理由；

（3）根据规律，是否存在一个正边形，使其中？若存在，直接写出的值；若不存在，请说明理由．

Answer 1

【答案】（1）60°，45°，36°，30°，12°；（2）存在，n=18；（3）不存在，理由见解析．

【解析】

（1）根据多边形内角和公式求出每个内角的度数，再根据三角形内角和及等腰三角形的性质求解即可；

（2）根据表中的结果得出规律，根据规律得出方程，求出方程的解即可；

（3）根据表中的结果得出规律，根据规律得出方程，求出方程的解即可．

解：（1）根据正多边形的内角和公式可知，正n边形的内角和=(n-2)×180°，故n边形一个内角度数=，

当正多边形有3条边时，一个内角度数==60°，则∠α==60°；

当正多边形有4条边时，一个内角度数==90°，则∠α==45°；

当正多边形有5条边时，一个内角度数==108°，则∠α==36°；

当正多边形有6条边时，一个内角度数==120°，则∠α==30°；

．．．

当正多边形有15条边时，内角度数==156°，则∠α==12°．

故答案为：60°，45°，36°，30°，12°；

（2）存在．

由（1）可知，，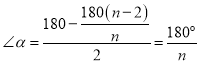

设存在正多边形使得，则，，

∴存在一个正多边形使；

（3）不存在，理由如下：

设存在多边形使得，则，（不是整数），

∴不存在一个多边形使．