题目内容
⊙O1与⊙O2的半径分别是R、r(R>r),且(
,0)、(
,0)是函数y=x2-3x+2与x轴的两个交点.且O1O2=
,
,则⊙O1与⊙O2的位置关系是( )
| 1 |
| R |
| 1 |
| r |
| 3 |
| 4 |
,则⊙O1与⊙O2的位置关系是( )
| A、外离 | B、内含 | C、相交 | D、外切 |
分析:由(
,0)、(
,0)是函数y=x2-3x+2与x轴的两个交点,得到
+
=3,
•
=2,进一步求出R+r和R-r的值,和O1O2的值比较即可得出答案.
| 1 |
| R |
| 1 |
| r |
| 1 |
| R |
| 1 |
| r |
| 1 |
| R |
| 1 |
| r |
解答:解:∵(
,0)、(
,0)是函数y=x2-3x+2与x轴的两个交点,
∴
+
=3,
•
=2,
解得:Rr=
,R+r=
,
R-r=
=
∵O1O2=
,
∴R-r<O1O2<r+R,
∴⊙O1与⊙O2的位置关系是相交.
故选C.
| 1 |
| R |
| 1 |
| r |
∴
| 1 |
| R |
| 1 |
| r |
| 1 |
| R |
| 1 |
| r |
解得:Rr=
| 1 |
| 2 |
| 3 |
| 2 |
R-r=
| (R+r)2-4Rr |
| 1 |
| 2 |
∵O1O2=
| 3 |
| 4 |
∴R-r<O1O2<r+R,
∴⊙O1与⊙O2的位置关系是相交.
故选C.
点评:本题主要考查了抛物线与x轴的交点,圆与圆的位置关系等知识点,求出R+r和R-r的值,并能和O1O2的值进行比较,确定两圆的位置关系是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
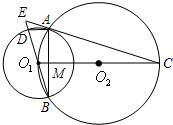 的延长线交于E点,AB与O1C相交于M点.
的延长线交于E点,AB与O1C相交于M点.