题目内容
【题目】如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB﹣BD做匀速运动,动点Q从点D同时出发,沿着线路DC﹣CB﹣BA做匀速运动.
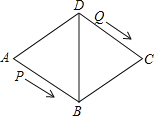
(1)求BD的长;
(2)已知动点P、Q运动的速度分别为8cm/s、10cm/s.经过12秒后,P、Q分别到达M、N两点,试判断△AMN的形状,并说明理由,同时求出△AMN的面积;
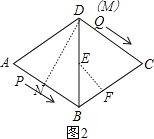
(3)设问题(2)中的动点P、Q分别从M、N同时沿原路返回,动点P的速度不变,动点Q的速度改变为a cm/s,经过3秒后,P、Q分别到达E、F两点,若△BEF为直角三角形,试求a的值.
【答案】(1)48cm;(2)288![]() (cm2);(3)若△BEF为直角三角形,a的值为4或12或24.
(cm2);(3)若△BEF为直角三角形,a的值为4或12或24.
【解析】
试题分析:(1)根据菱形的性质得AB=BC=CD=AD=48,加上∠A=60°,于是可判断△ABD是等边三角形,所以BD=AB=48;
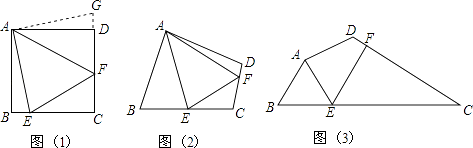
(2)如图1,根据速度公式得到12秒后点P走过的路程为96cm,则点P到达点D,即点M与D点重合,12秒后点Q走过的路程为120cm,而BC+CD=96,易得点Q到达AB的中点,即点N为AB的中点,根据等边三角形的性质得MN⊥AB,即△AMN为直角三角形,然后根据等边三角形面积可计算出S△AMN=288![]() cm2;
cm2;
(3)由△ABD为等边三角形得∠ABD=60°,根据速度公式得经过3秒后点P运动的路程为24cm、点Q运动的路程为3acm,所以BE=DE=24cm,
然后分类讨论:当点Q运动到F点,且点F在NB上,如图1,则NF=3a,BF=BN﹣NF=24﹣3a,由于△BEF为直角三角形,而∠FBE=60°,只能得到∠EFB=90°,所以∠FEB=30°,根据含30度的直角三角形三边的关系得24﹣3a=![]() ×24,解得a=4;当点Q运动到F点,且点F在BC上,如图2,则NF=3a,BF=BN﹣NF=3a﹣24,由于△BEF为直角三角形,而∠FBE=60°,若∠EFB=90°,则∠FEB=30°,根据含30度的直角三角形三边的关系得3a﹣24=
×24,解得a=4;当点Q运动到F点,且点F在BC上,如图2,则NF=3a,BF=BN﹣NF=3a﹣24,由于△BEF为直角三角形,而∠FBE=60°,若∠EFB=90°,则∠FEB=30°,根据含30度的直角三角形三边的关系得3a﹣24=![]() ×24,解得a=12;若∠EFB=90°,易得此时点F在点C处,则3a=24+48,解得a=24.
×24,解得a=12;若∠EFB=90°,易得此时点F在点C处,则3a=24+48,解得a=24.
解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD=48,
∵∠A=60°,
∴△ABD是等边三角形,
∴BD=AB=48,
即BD的长是48cm;
(2)如图1,12秒后点P走过的路程为8×12=96,则12秒后点P到达点D,即点M与D点重合,
12秒后点Q走过的路程为10×12=120,而BC+CD=96,所以点Q到B点的距离为120﹣96=24,则点Q到达AB的中点,即点N为AB的中点,
∵△ABD是等边三角形,而MN为中线,
∴MN⊥AB,
∴△AMN为直角三角形,
∴S△AMN=![]() S△ABD=
S△ABD=![]() ×
×![]() ×482=288
×482=288![]() (cm2);
(cm2);
(3)∵△ABD为等边三角形,
∴∠ABD=60°,
经过3秒后,点P运动的路程为24cm、点Q运动的路程为3acm,
∵点P从点M开始运动,即DE=24cm,
∴点E为DB的中点,即BE=DE=24cm,
当点Q运动到F点,且点F在NB上,如图1,则NF=3a,
∴BF=BN﹣NF=24﹣3a,
∵△BEF为直角三角形,
而∠FBE=60°,
∴∠EFB=90°(∠FEB不能为90°,否则点F在点A的位置),
∴∠FEB=30°,
∴BF=![]() BE,
BE,
∴24﹣3a=![]() ×24,
×24,
∴a=4;
当点Q运动到F点,且点F在BC上,如图2,则NF=3a,
∴BF=BN﹣NF=3a﹣24,
∵△BEF为直角三角形,
而∠FBE=60°,
若∠EFB=90°,则∠FEB=30°,
∴BF=![]() BE,
BE,
∴3a﹣24=![]() ×24,
×24,
∴a=12;
若∠EFB=90°,即FB⊥BD,
而DE=BE,
∴点F在BD的垂直平分线上,
∴此时点F在点C处,
∴3a=24+48,
∴a=24,
综上所述,若△BEF为直角三角形,a的值为4或12或24.


【题目】心理学家研究发现,一般情况下,学生的注意力随着教师讲课时间的变化而变化,讲课开始时学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散,经过实验分析可知,一般地,学生的注意力y随时间t的变化情况如下表:

上课时间t(分) | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
学生的注意力y | 100 | 191 | 240 | 240 | 240 | 205 | 170 | 135 | 100 | 65 |
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中?
(2)从表中观察,讲课开始后,学生的注意力最集中的时间是那一段?
(3)从表中观察,讲课开始后,学生的注意力从第几分钟起开始下降?猜想注意力下降过程中y与t的关系,并用式子表示出来。
用(3)题中的关系式,求当t=27分时,学生的注意力y的值是多少。现有一道数学难题,需要讲解20分钟,为了效果更好,要求学生的注意力最低达到190,那么老师能否在学生注意力达到所需状态下讲完这道题目,试着说明理由。