Question

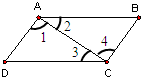
已知：如图，DC∥AB，DF平分∠CDB，BE平分∠ADB．
求证：∠1=∠2
证明：∵DC∥AB，

已知

∴∠ABD=∠CDB．

两直线平行，内错角相等

∵DF平分∠CDB，

已知

BE平分∠CDB，

已知

∴∠1=

1

2

∠_------，

∠CDB角平分线定义

∴∠2=

1

2

∠_------，

∠ABD，角平分线定义

∴∠1=∠2．

Answer 1

分析：先根据平行线的性质得出∠ABD=∠CDB，再由DF平分∠CDB，BE平分∠CDB可知∠1=

1

2

∠CDB，∠2=

1

2

∠ABD，故可得出∠1=∠2．

解答：证明：∵DC∥AB，
∴∠ABD=∠CDB．
∵DF平分∠CDB，BE平分∠CDB，
∴∠1=

1

2

∠CDB，
∴∠2=

1

2

∠ABD，
∴∠1=∠2．

点评：本题考查的是平行线的性质及角平分线的定义，用到的知识点为：两直线平行，内错角相等．