题目内容
等腰直角三角形的斜边长是有理数,则面积S是( )理数,周长l是( )理数.
| A、有,有 | B、无,无 | C、有,无 | D、无,有 |
分析:由等腰直角三角形的性质可得,直角边=
,从而可得出面积S及周长l的表达式,进而判断出答案.
| 斜边 | ||
|
解答:解:设等腰三角形的斜边为c,
则可求得直角边为
,
∴s=
×
×
=
,为有理数;l=
+
+c=
c+c,为无理数.
故选C.
则可求得直角边为
| c | ||
|
∴s=
| 1 |
| 2 |
| c | ||
|
| c | ||
|
| c2 |
| 4 |
| c | ||
|
| c | ||
|
| 2 |
故选C.
点评:本题考查了三角形的三边关系,关键是根据等腰直角三角形的性质得出三角形的两条直角边,表示出面积及周长后,要注意判断是无理数还是有理数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
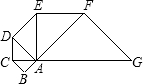 已知△ABC是斜边长为1cm的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是( )
已知△ABC是斜边长为1cm的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,第n个等腰直角三角形的斜边长是( )A、
| ||
B、
| ||
| C、2ncm | ||
D、
|
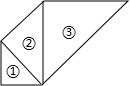 如图,以第①个等腰直角三角形的斜边长作为第②个等腰直角三角形的腰,以第②个等腰直角三角形的斜边长做为第③个等腰直角三角形的腰,依此类推,若第⑨个等腰直角三角形的斜边长为
如图,以第①个等腰直角三角形的斜边长作为第②个等腰直角三角形的腰,以第②个等腰直角三角形的斜边长做为第③个等腰直角三角形的腰,依此类推,若第⑨个等腰直角三角形的斜边长为

 如图,AB是等腰直角三角形的斜边,若点M在边AC上,点N在边BC上,沿直线MN将△MCN翻折,使点C落在AB上,设其落点为点P.当点P是边AB的中点时,求证:
如图,AB是等腰直角三角形的斜边,若点M在边AC上,点N在边BC上,沿直线MN将△MCN翻折,使点C落在AB上,设其落点为点P.当点P是边AB的中点时,求证: