题目内容
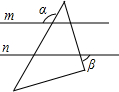 小明同学把一个含有45°角的直角三角板放在如图所示的两条平行线m、n上,测得∠α=120°,则∠β的度数是
小明同学把一个含有45°角的直角三角板放在如图所示的两条平行线m、n上,测得∠α=120°,则∠β的度数是
- A.45°
- B.55°
- C.65°
- D.75°
D
分析:根据行线的性质得∠1=∠2,根据三角形外角性质有∠α=∠2+∠3,可计算出∠2=120°-45°=75°,则∠1=75°,根据对顶角相等即可得到∠β的度数.
解答:如图,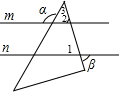
∵m∥n,
∴∠1=∠2,
∵∠α=∠2+∠3,
而∠3=45°,∠α=120°,
∴∠2=120°-45°=75°,
∴∠1=75°,
∴∠β=75°.
故选D.
点评:本题考查了平行线的性质:两直线平行,同位角相等.也考查了三角形外角性质以及对顶角的性质.
分析:根据行线的性质得∠1=∠2,根据三角形外角性质有∠α=∠2+∠3,可计算出∠2=120°-45°=75°,则∠1=75°,根据对顶角相等即可得到∠β的度数.
解答:如图,

∵m∥n,
∴∠1=∠2,
∵∠α=∠2+∠3,
而∠3=45°,∠α=120°,
∴∠2=120°-45°=75°,
∴∠1=75°,
∴∠β=75°.
故选D.
点评:本题考查了平行线的性质:两直线平行,同位角相等.也考查了三角形外角性质以及对顶角的性质.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
小明同学把一个含有45°角的直角三角板放在如图所示的两条平行线m,n上,测得 =120°,则
=120°,则 的度数是
的度数是
| A.45° | B.55° | C.65° | D.75° |
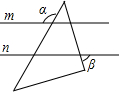 (2012•海南)小明同学把一个含有45°角的直角三角板放在如图所示的两条平行线m、n上,测得∠α=120°,则∠β的度数是( )
(2012•海南)小明同学把一个含有45°角的直角三角板放在如图所示的两条平行线m、n上,测得∠α=120°,则∠β的度数是( ) =120°,则
=120°,则 的度数是
的度数是
 上,测得
上,测得 ,则
,则 的度数是【 】
的度数是【 】
